题目内容
 如图,P是△ABC中边AB上一点,连接CP,有如下条件:①∠ACP=∠B,②∠APC=∠ACB,③AC2=AP•AB,④
如图,P是△ABC中边AB上一点,连接CP,有如下条件:①∠ACP=∠B,②∠APC=∠ACB,③AC2=AP•AB,④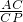 =
= ,其中能判定△ACP∽△ABC的条件是________(填序号).
,其中能判定△ACP∽△ABC的条件是________(填序号).
①②③
分析:根据图形,∠A为△ACP和△ABC的公共角,然后根据相似三角形的判定方法对各小题分析判断后利用排除法求解.
解答:由图可知,∠A为△ACP和△ABC的公共角,
①∠ACP=∠B,符合两角对应相等,两三角形相似,
②∠APC=∠ACB,符合两角对应相等,两三角形相似,
③由AC2=AP•AB可得 =
= ,符合两边对应成比例,夹角相等,两三角形相似,
,符合两边对应成比例,夹角相等,两三角形相似,
④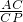 =
= ,夹角为∠B,可判定△CBP∽△ABC,
,夹角为∠B,可判定△CBP∽△ABC,
所以能判定△ACP∽△ABC的条件是①②③.
故答案为:①②③.
点评:本题考查了相似三角形的判定,熟记三角形的判定方法是解题的关键.
分析:根据图形,∠A为△ACP和△ABC的公共角,然后根据相似三角形的判定方法对各小题分析判断后利用排除法求解.
解答:由图可知,∠A为△ACP和△ABC的公共角,
①∠ACP=∠B,符合两角对应相等,两三角形相似,
②∠APC=∠ACB,符合两角对应相等,两三角形相似,
③由AC2=AP•AB可得
 =
= ,符合两边对应成比例,夹角相等,两三角形相似,
,符合两边对应成比例,夹角相等,两三角形相似,④
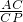 =
= ,夹角为∠B,可判定△CBP∽△ABC,
,夹角为∠B,可判定△CBP∽△ABC,所以能判定△ACP∽△ABC的条件是①②③.
故答案为:①②③.
点评:本题考查了相似三角形的判定,熟记三角形的判定方法是解题的关键.

练习册系列答案
相关题目
 8、如图,DE是△ABC中边AC的垂直平分线,若BC=18cm,AB=10cm,则△ABD的周长为( )
8、如图,DE是△ABC中边AC的垂直平分线,若BC=18cm,AB=10cm,则△ABD的周长为( ) 13、如图,AD是△ABC中BC边上的中线,E,F分别是AD、BE的中点,若△BFD的面积为6,则△ABC的面积等于
13、如图,AD是△ABC中BC边上的中线,E,F分别是AD、BE的中点,若△BFD的面积为6,则△ABC的面积等于 如图,D是△ABC中AC边上的一点,根据下列条件不可推出△BDC∽△ABC的是( )
如图,D是△ABC中AC边上的一点,根据下列条件不可推出△BDC∽△ABC的是( ) 如图,D是△ABC中BC边上一点,AB=AC=BD,AD=DC,则∠B的度数是( )
如图,D是△ABC中BC边上一点,AB=AC=BD,AD=DC,则∠B的度数是( ) 如图,P是△ABC中∠B,∠C两角平分线的交点,过点P作DE∥BC,分别与AB、AC交于点D、E,DE=10,则DB+EC=
如图,P是△ABC中∠B,∠C两角平分线的交点,过点P作DE∥BC,分别与AB、AC交于点D、E,DE=10,则DB+EC=