题目内容
如图，∠D=90°，BC=10，∠CBD=30°，∠A=15°．
（1）求CD的长；
（2）求tanA的值．
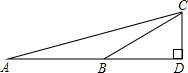
（1）求CD的长；
（2）求tanA的值．
（1）在Rt△BDC中，∠D=90°，BC=10，∠CBD=30°，
∴CD=BC•sin30°=10×
=5；
（2）在Rt△BDC中，∠D=90°，BC=10，∠CBD=30°，
∵cos30°=
，
∴BD=BC•cos30°=10×
=5
．
∵∠CBD=30°，∠A=15°，
∴∠A=∠ACB，
．∴AB=BC=10．
∴在Rt△CAD中，tanA=
=
=
=2-
．
∴CD=BC•sin30°=10×
| 1 |
| 2 |
（2）在Rt△BDC中，∠D=90°，BC=10，∠CBD=30°，
∵cos30°=
| BD |
| BC |
∴BD=BC•cos30°=10×
| ||
| 2 |
| 3 |
∵∠CBD=30°，∠A=15°，
∴∠A=∠ACB，
．∴AB=BC=10．
∴在Rt△CAD中，tanA=
| CD |
| AD |
| 5 | ||
10+5
|
| 1 | ||
2+
|
| 3 |
练习册系列答案
阅读快车系列答案
相关题目
一点B，以B为圆心，180m为半径的圆形区域是一个奶牛养殖场．在AD上取一点C，测得AC=200m，点B在点C的北偏西75°方向上．
