题目内容
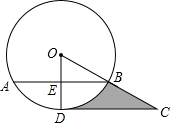如图，点D在⊙O上，且CD⊥OD于点D，连结OC，交⊙O于点B，过点B作弦AB⊥OD，点E为垂足，已知⊙O的半径为12，∠COD=60°．
（1）求弦AB的长．
（2）阴影部分的面积．
解：（1）∵CD切⊙O点D，
∴CD⊥OD，
又∵AB⊥OD，
∴BE=AE
∵∠COD=60°，OB=12，
∴sin∠COD=
=
，
∴BE=6
，
∴AB=12；
（2）S阴=S△ODC-S扇形ODB=
×12×12-
=72-24π．
分析：（1）由弦AB⊥OD，根据三角函数的性质与垂径定理，即可求得弦AB的长；
（2）由S阴=S扇形BOD-S△BOE，即可求得答案．
点评：此题考查了切线的性质、垂径定理、扇形的面积以及三角函数的性质．此题难度不大，注意掌握数形结合思想的应用．
∴CD⊥OD，
又∵AB⊥OD，
∴BE=AE
∵∠COD=60°，OB=12，
∴sin∠COD=
=，∴BE=6
，∴AB=12
；（2）S阴=S△ODC-S扇形ODB=
×12×12-=72-24π．分析：（1）由弦AB⊥OD，根据三角函数的性质与垂径定理，即可求得弦AB的长；
（2）由S阴=S扇形BOD-S△BOE，即可求得答案．
点评：此题考查了切线的性质、垂径定理、扇形的面积以及三角函数的性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
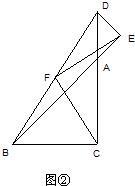
27、附加题：
如图，点D在AB上，DF交AC于点E，CF∥AB，AE=EC．
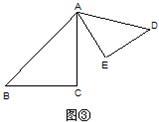
如图，点D在AB上，直线DG交AF于点E．请从①DG∥AC，②AF平分∠BAC，③AD=DE中任选两个作为条件，余下一个作为结论，构造一个真命题，并说明理由．已知：