题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() .
.
(1)如图1,![]() 与
与![]() 的数量关系是________;
的数量关系是________;

(2)如图2,若![]() 是线段
是线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() ,请猜想
,请猜想![]() 、
、![]() 、
、![]() 三者之间的数量关系,并证明你的结论;
三者之间的数量关系,并证明你的结论;

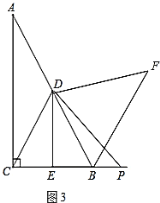
(3)若点![]() 是线段
是线段![]() 延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出
延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出![]() 、
、![]() 、
、![]() 三者之间的数量关系.
三者之间的数量关系.

【答案】(1)![]() ;(2)
;(2)![]()
![]() ,证明见解析;(3)作图见解析,
,证明见解析;(3)作图见解析,![]()
![]()
【解析】
(1)由∠ACB=90°,∠A=30°得到∠B=60°,根据直角三角形斜边上中线性质得到DB=DC,则可判断△DCB为等边三角形,由于DE⊥BC,DE=![]() BC;
BC;
(2)根据旋转的性质得到∠PDF=60°,DP=DF,易得∠CDP=∠BDF,则可根据“SAS”可判断△DCP≌△DBF,则CP=BF,利用CP=BC-BP,DE=![]() BC可得到
BC可得到![]()
![]() ;
;
(3)与(2)的证明方法一样得到△DCP≌△DBF得到CP=BF,而CP=BC+BP,则BF-BP=BC,所以![]()
![]()
![]() .
.
解:(1)∵![]() ,
,![]()
∴![]()
∵点![]() 是
是![]() 的中点,
的中点,
∴![]()
∴![]() 为等边三角形,
为等边三角形,
∵![]() ,
,
∴![]()
(2)∵线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]()
∴![]() ,
,![]() ,
,
∴![]()
即![]()
在![]() 与
与![]() 中
中
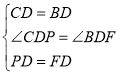
∴![]()
∴![]()
由(1)知:
![]()
![]()
![]()
(3)![]()
∴![]()
即![]()
在![]() 和
和![]() 中
中
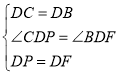
∴![]()
∴![]()
而CP=BC+BP,
∴BF-BP=BC,
![]()
![]()
![]()

【题目】某学校组织了“热爱宪法,捍卫宪法”的知识竞赛,赛后发现所有学生的成绩(总分100分)均不低于50分,为了解本次竞赛的成绩分布情况,随机抽取若干名学生的成绩作为样本进行整理,并绘制了不完整的统计图表,请你根据统计图表解答下列问题.
学校若干名学生成绩分布统计表
分数段(成绩为x分) | 频数 | 频率 |
50≤x<60 | 16 | 0.08 |
60≤x<70 | a | 0.31 |
70≤x<80 | 72 | 0.36 |
80≤x<90 | c | d |
90≤x≤100 | 12 | b |
(1)此次抽样调查的样本容量是 ;
(2)写出表中的a= ,b= ,c= ;
(3)补全学生成绩分布直方图;
(4)比赛按照分数由高到低共设置一、二、三等奖,若有25%的参赛学生能获得一等奖,则一等奖的分数线是多少?





