Question

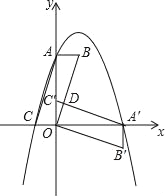
【题目】如图，在平面直角坐标系中，平行四边形ABOC如图放置，将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′．抛物线y＝﹣x2+2x+3经过点A、C、A′三点．

（1）求A、A′、C三点的坐标；

（2）求平行四边形ABOC和平行四边形A′B′OC′重叠部分△C′OD的面积；

（3）点M是第一象限内抛物线上的一动点，问点M在何处时，△AMA′的面积最大？最大面积是多少？并写出此时M的坐标．

Answer 1

【答案】（1）C（﹣1，0），A′（3，0），A（0，3）；（2）；（3）S△AMA′＝＝﹣（m﹣）2+，∴当m＝时，S△AMA'的值最大，最大值为，此时M点坐标为（，）．

【解析】

（1）利用抛物线与x轴的交点问题可求出C（﹣1，0），A′（3，0）；计算自变量为0时的函数值可得到A（0，3）；

（2）先由平行四边形的性质得AB∥OC，AB＝OC，易得B（1，3），根据勾股定理和三角形面积公式得到OB＝，S△AOB＝，再根据旋转的性质得∠ACO＝∠OC′D，OC′＝OC＝1，接着证明△C′OD∽△BOA，利用相似三角形的性质得＝()2，则可计算出S△C′OD；

（3）根据二次函数图象上点的坐标特征，设M点的坐标为（m，﹣m2+2m+3），0＜m＜3，作MN∥y轴交直线AA′于N，求出直线AA′的解析式为y＝﹣x+3，则N（m，﹣m+3），于是可计算出MN＝﹣m2+3m，再利用S△AMA′＝S△ANM+S△MNA′和三角形面积公式得到S△AMA′＝﹣m2+m，然后根据二次函数的最值问题求出△AMA′的面积最大值，同时即可确定此时M点的坐标．

（1）当y＝0时，﹣x2+2x+3＝0，

解得x1＝3，x2＝﹣1，

则C（﹣1，0），A′（3，0），

当x＝0时，y＝3，则A（0，3）；

（2）∵四边形ABOC为平行四边形，

∴AB∥OC，AB＝OC，

而C（﹣1，0），A（0，3），

∴B（1，3），

∴OB＝＝，S△AOB＝×3×1＝，

又∵平行四边形ABOC旋转90°得平行四边形A′B′OC′，

∴∠ACO＝∠OC′D，OC′＝OC＝1，

又∵∠ACO＝∠ABO，

∴∠ABO＝∠OC′D．

又∵∠C′OD＝∠AOB，

∴△C′OD∽△BOA，

∴＝()2＝（）2＝ ，

∴S△C′OD＝×＝；

（3）设M点的坐标为（m，﹣m2+2m+3），0＜m＜3，

作MN∥y轴交直线AA′于N，易得直线AA′的解析式为y＝﹣x+3，则N（m，﹣m+3），

∵MN＝﹣m2+2m+3﹣（﹣m+3）＝﹣m2+3m，

∴S△AMA′＝S△ANM+S△MNA′

＝MN3

＝（﹣m2+3m）

＝﹣m2+m

＝﹣（m﹣）2+，

∴当m＝时，S△AMA'的值最大，最大值为，此时M点坐标为（，）．