题目内容
如图，l1∥l2，l3⊥l4，∠1=42°，那么∠2的度数为
- A.48°
- B.42°
- C.38°
- D.21°
A
分析：先根据两直线平行，同位角相等求出∠3，再根据直角三角形两锐角互余即可求出∠2．
解答：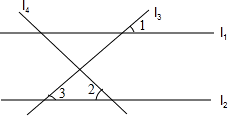
解：如图，∵l1∥l2，∠1=42°，
∴∠3=∠1=42°，
∵l3⊥l4，
∴∠2=90°-∠3=48°．
故选A．
点评：本题利用平行线的性质和直角三角形两锐角互余的性质．
分析：先根据两直线平行，同位角相等求出∠3，再根据直角三角形两锐角互余即可求出∠2．
解答：
解：如图，∵l1∥l2，∠1=42°，∴∠3=∠1=42°，
∵l3⊥l4，
∴∠2=90°-∠3=48°．
故选A．
点评：本题利用平行线的性质和直角三角形两锐角互余的性质．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
13、如图，l1∥l2，∠1=120°，∠2=100°，则∠3=（ ）
如图，l1∥l2，AB⊥AC，∠ABC=50°，则∠1=（ ）度．
如图，l1∥l2∥l3，已知L1与l3之间的距离为8cm，l1与l2之间的距离为3cm，则l2与l3之间的距离为
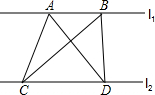如图，l1∥l2，A、B为直线l1上两点，C、D为直线l2上两点，则△ACD与△BCD的面积大小关系是（ ）| A、S△ACD＜S△BCD | B、S△ACD=S△BCD | C、S△ACD＞S△BCD | D、不能确定 |