题目内容
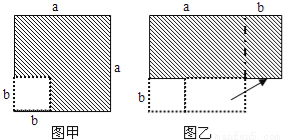
在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )
A. (a+b)2=a2+2ab+b2
B. (a﹣b)2=a2﹣2ab+b2
C. a2﹣b2=(a+b)(a﹣b)
D. (a+2b)(a﹣b)=a2+ab﹣2b2
C 【解析】根据两个图形的特征结合正方形、长方形的面积公式求解即可. 【解析】 ∵图甲中阴影部分的面积=a2﹣b2,图乙中阴影部分的面积=(a+b)(a﹣b), 而两个图形中阴影部分的面积相等, ∴阴影部分的面积=a2﹣b2=(a+b)(a﹣b). 故选C. “点睛”本题主要考查了乘法的平方差公式,属于基础应用题,只需学生熟练掌握正方形、长方形的面积公式,即可...
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目


 轴交于点
轴交于点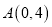 ,与
,与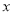 轴交于
轴交于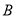 、
、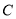 两点,其中
两点,其中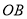 、
、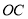 是方程的
是方程的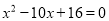 两根,且
两根,且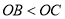 .
. )求抛物线的解析式;
)求抛物线的解析式; )直线
)直线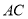 上是否存在点
上是否存在点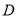 ,使
,使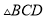 为直角三角形.若存在,求所有
为直角三角形.若存在,求所有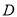 点坐标;反之说理;
点坐标;反之说理;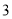 )点
)点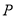 为
为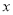 轴上方的抛物线上的一个动点(
轴上方的抛物线上的一个动点(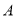 点除外),连
点除外),连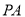 、
、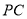 ,若设
,若设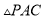 的面积为
的面积为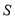 .
. 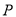 点横坐标为
点横坐标为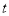 ,则
,则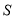 在何范围内时,相应的点
在何范围内时,相应的点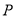 有且只有
有且只有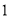 个.
个.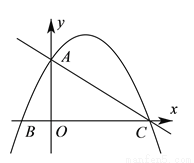
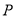 ,羽毛球飞行的水平距离
,羽毛球飞行的水平距离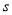 (米)与其距地面高度
(米)与其距地面高度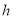 (米)之间的关系式为
(米)之间的关系式为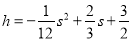 ,如图,已知球网
,如图,已知球网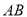 距原点
距原点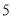 米,乙(用线段
米,乙(用线段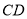 表示)扣球的最大高度为
表示)扣球的最大高度为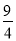 米,设乙的起跳点
米,设乙的起跳点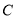 的横坐标为
的横坐标为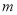 ,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则
,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则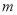 的取值范围是__________.
的取值范围是__________.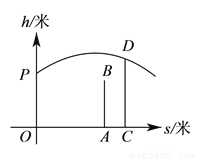
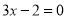 B.
B. 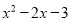 C.
C. 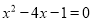 D.
D. 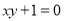
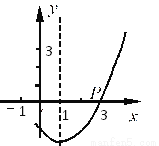
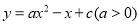 的对称轴是直线
的对称轴是直线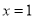 ,且图像经过点
,且图像经过点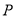 (3,0),则
(3,0),则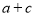 的值为( )
的值为( )