Question

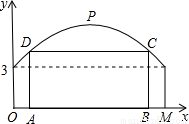
如图，某隧道横截面的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成，最大高度为6米，底部宽度为12米．现以O点为原点，OM所在直线为x轴建立直角坐标系．

（1）直接写出点M及抛物线顶点P的坐标； （2）求出这条抛物线的函数解析式； （3）若要搭建一个矩形"支撑架"AD-DC-CB，使C、D点在抛物线上，A、B点在地面OM上，则这个"支撑架"总长的最大值是多少？

Answer 1

(1) M(12，0)，P(6，6) (2) 设此函数关系式为：∵函数经过点(0，3)， ∴即， ∴此函数解析式为： (3) 设A(m，0)，则B(12-m，0)，C，D ∴"支撑架"总长：AD+DC+CB =                                               = ∵＜0   ∴ 当m = 0时，AD+DC+CB有最大值为18。