题目内容
【题目】如图，在
中，
，
，
，
是
的中点，点
在边
上，将
沿
翻折，使点
落在点
处，当
时，
________．
【答案】
或
【解析】
分两种情况进行讨论：①当
在
上方时，由折叠可得
，当
时，
，再过点
作
于点
，过点
作
于点
，则
是等腰三角形，再根据
、是
的中点、
求得
、
，最后根据等腰
中，
，即可得到结论；②当在下方时，同样是作辅助线构造等腰直角三角形和矩形，利用勾股定理进行计算求解．
解：①当在上方时
∵在
中，
，
，
∴
∵由折叠可得
∴当时，
过点作于点，过点作于点，如图：
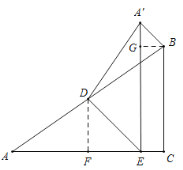
∴是等腰直角三角形
∵、是的中点、
∴
，
∴，
∴矩形
中，
，
∵
∴
∴
∴
∴等腰中，
；
②当在下方时
∵由折叠可得
∴当时，
，
∴
过点作于点，过点作
于点，如图：
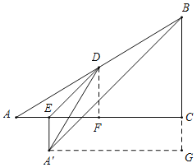
∴是等腰直角三角形
∴
∵
∴
，
∵
∴
∴
∴
∴等腰中，
．
∴综上所述，
或．
故答案是：或
练习册系列答案
口算题天天练系列答案
相关题目
