题目内容
 如图,已知:△ABC中,BD、CE分别是AC、AB边上的高,G、F分别是BC、DE的中点.试探索FG与DE的关系.
如图,已知:△ABC中,BD、CE分别是AC、AB边上的高,G、F分别是BC、DE的中点.试探索FG与DE的关系.分析:FG⊥DE,连接GD、GE,根据直角三角形斜边上的中线等于斜边的一半可得GD=
BC=GE,再根据等腰三角形三线合一的性质即可证得结论.
| 1 |
| 2 |
解答:解:FG垂直平分DE,
理由如下:连接GD、GE.
∵BD是△ABC的高,G为BC的中点,
∴在Rt△CBD中,GD=
BC,(直角三角形斜边上的中线等于斜边的一半)
同理可得GE=
BC,
∴GD=GE,
∵F是DE的中点(等腰三角形三线合一),
∴FG⊥DE.

理由如下:连接GD、GE.
∵BD是△ABC的高,G为BC的中点,
∴在Rt△CBD中,GD=
| 1 |
| 2 |
同理可得GE=
| 1 |
| 2 |
∴GD=GE,
∵F是DE的中点(等腰三角形三线合一),
∴FG⊥DE.
点评:此题主要考查等腰三角形的性质及直角三角形斜边上的中线的性质的综合运用.

练习册系列答案
相关题目
 如图,已知:△ABC中,∠1=∠2,且AE=AD,BE和CD相交于F.求证:BF=CF.
如图,已知:△ABC中,∠1=∠2,且AE=AD,BE和CD相交于F.求证:BF=CF. 如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE.
如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE. 如图,已知在△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,则
如图,已知在△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,则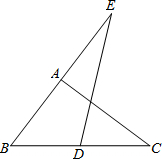 如图,已知在△ABC中,D是边BC的中点,点E在边BA的延长线上,AE=AB,
如图,已知在△ABC中,D是边BC的中点,点E在边BA的延长线上,AE=AB,