题目内容
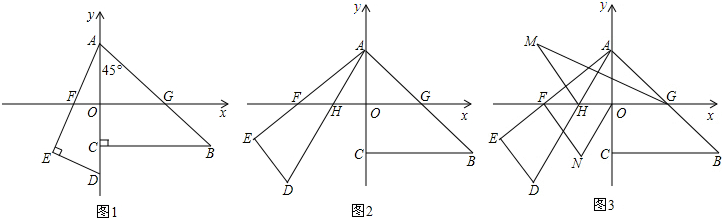
在图中,把一副直角三角板ABC和EFG(其短直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕点O顺时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).(1)在上述旋转过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?证明你发现的结论;
(2)连接HK,在上述旋转过程中,设BH=x,△GKH的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的
| 1 | 16 |
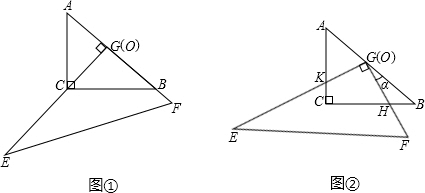
分析:(1)首先证明△BGH≌△CGK,然后根据S四边形CHGK=S△CHG+S△CGK=S△CHG+S△BGH=
S△ABC即可求解;
(2)根据S△GHK=S四边形CHGK-S△CHK即可列出函数解析式;
(3)转化为方程问题,利用根的判别式即可确定.
| 1 |
| 2 |
(2)根据S△GHK=S四边形CHGK-S△CHK即可列出函数解析式;
(3)转化为方程问题,利用根的判别式即可确定.
解答:解:(1)在上述旋转过程中,BH=CK,四边形CHGK的面积不变.
证明:连接CG
∵△ABC为等腰直角三角形,O(G)为斜边AB中点,
∴CG=BG,CG⊥AB.
∴∠ACG=∠B=45°,
∵∠BGH与∠CGK均为旋转角,
∴∠BGH=∠CGK.
∴△BGH≌△CGK.(3分)
∴BH=CK,S△BGH=S△CGK.
∴S四边形CHGK=S△CHG+S△CGK=S△CHG+S△BGH=
S△ABC=
×
×4×4=4.
即:S四边形CHGK的面积为4,是一个定值,在旋转过程中没有变化.(4分)
(2)∵AC=BC=4,BH=x,
∴CH=4-x,CK=x.
由S△GHK=S四边形CHGK-S△CHK,
得,y=4-
x(4-x)
∴y=
x2-2x+4.
∵0°<α<90°,
∴0<x<4.(6分)
(3)不存在.
根据题意,得
x2-2x+4=
×8.
化简,得 x2-4x+7=0.
∵△=16-4×1×7<0,
∴此方程无实数根.
即不存在这样的位置,使△GKH的面积等于△ABC面积的
.(8分)
证明:连接CG
∵△ABC为等腰直角三角形,O(G)为斜边AB中点,
∴CG=BG,CG⊥AB.
∴∠ACG=∠B=45°,
∵∠BGH与∠CGK均为旋转角,
∴∠BGH=∠CGK.
∴△BGH≌△CGK.(3分)
∴BH=CK,S△BGH=S△CGK.
∴S四边形CHGK=S△CHG+S△CGK=S△CHG+S△BGH=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即:S四边形CHGK的面积为4,是一个定值,在旋转过程中没有变化.(4分)

(2)∵AC=BC=4,BH=x,
∴CH=4-x,CK=x.
由S△GHK=S四边形CHGK-S△CHK,
得,y=4-
| 1 |
| 2 |
∴y=
| 1 |
| 2 |
∵0°<α<90°,
∴0<x<4.(6分)
(3)不存在.
根据题意,得
| 1 |
| 2 |
| 1 |
| 16 |
化简,得 x2-4x+7=0.
∵△=16-4×1×7<0,
∴此方程无实数根.
即不存在这样的位置,使△GKH的面积等于△ABC面积的
| 1 |
| 16 |
点评:本题主要考查了旋转的性质,函数的解析式的求解,以及一元二次方程的根的判别式,难度较大.

练习册系列答案
相关题目