题目内容
如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)图(1),当t为何值时,AP=2AQ;
(2)图(2),当t为何值时,△APQ为直角三角形;
(3) 图(3),作QD∥AB交BC于点D,连接PD,当t为何值时,△BDP与△PDQ相似?

图(1) 图(2) 图(3)
解:(1)△BPQ是等边三角形
当t时AP=6-t AQ=2t ∴6-t=2t ∴t=2
(2))∵QD∥BA∴∠QRC=∠A=60°,∠DQC=∠B=60° ∴△QDC是等边三角形
∴QD=DC=QC=6﹣2t ∵BE=BQ•cos60°=![]() ×2t=t
×2t=t
∴EP=AB﹣AP﹣BE=6﹣t﹣t=6﹣2t ∴EP∥QD,EP=QD ∴四边形EPRQ是平行四边形
∴PD=EQ=![]() t 又∵∠PEQ=90°,∴∠APR=∠PRQ=90°
t 又∵∠PEQ=90°,∴∠APR=∠PRQ=90°
∵△APD∽△PDQ,∴∠QPD=∠A=60° ∴tan60°=![]() 即
即![]() 解得t=
解得t=![]()
∴当t=![]() 时,△APR∽△PRQ.
时,△APR∽△PRQ.


练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 的坐标为(-1,0).
的坐标为(-1,0). 如图,已知△ABC是等边三角形,AB交⊙O于点D,DE⊥AC于点E.
如图,已知△ABC是等边三角形,AB交⊙O于点D,DE⊥AC于点E.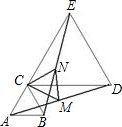 如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,
如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点, (2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
(2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF. (2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.
(2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.