题目内容
【题目】如图,△ABC中,AC=BC=10 cm,AB=12 cm,点D是AB的中点,连结CD,动点P从点A出发,沿A→C→B的路径运动,到达点B时运动停止,速度为每秒2 cm,设运动时间为![]() 秒.
秒.
(1)求CD的长;
(2)当![]() 为何值时,△ADP是直角三角形?
为何值时,△ADP是直角三角形?
(3)直接写出:当![]() 为何值时,△ADP是等腰三角形?
为何值时,△ADP是等腰三角形?
【答案】(1)8;(2)1.8;(3)1.8或5;(3)当![]() 或
或![]() 或
或![]() 或
或![]() 时,△ADP是等腰三角形.
时,△ADP是等腰三角形.
【解析】试题分析:(1)根据题意,运用等腰三角形的性质,求得AD的长,再根据勾股定理求得CD的长即可;
(2)分两种情况进行讨论:当DP⊥AC时,△ADP是直角三角形,当PD⊥AD时,△ADP是直角三角形,分别根据相似三角形的性质求解即可;
(3)分三种情况进行讨论:当PA=PD时,当AP=AD时,当AD=PD时,分别做辅助线构造三角形,运用速度、路程、时间的关系,求得t的值即可.
试题解析:解:(1)∵AB=12 cm,点D是AB的中点
∴![]()
∵AC=BC,点D是AB的中点
∴![]()
在![]() 中,
中, ![]()
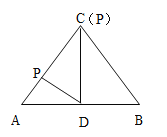
(2)当![]() 为直角三角形时,有两种情况,分别为:
为直角三角形时,有两种情况,分别为:
①当![]() 时,即点P在AC边上
时,即点P在AC边上
由![]() ,得
,得![]()
在![]() 中,
中, ![]()
∴![]()
②当![]() 时,点P与点C重合如图,
时,点P与点C重合如图,
此时, ![]() (秒)
(秒)
∴ 当![]() 为1.8秒或5秒时,△ADP是直角三角形.
为1.8秒或5秒时,△ADP是直角三角形.
(3)当![]() 或
或![]() 或
或![]() 或
或![]() 时,△ADP是等腰三角形.
时,△ADP是等腰三角形.

练习册系列答案
相关题目