题目内容
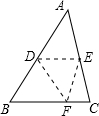
 如图,将三角形纸片的一角折叠,使点B落的AC边上的F处,折痕为DE,已知AB=AC=6,BC=8,若以点E,F,C为顶点的三角形与△ABC相似,那么BE的长是________.
如图,将三角形纸片的一角折叠,使点B落的AC边上的F处,折痕为DE,已知AB=AC=6,BC=8,若以点E,F,C为顶点的三角形与△ABC相似,那么BE的长是________.
 或4
或4分析:设BE=x,根据翻折的性质可得EF=CE=x,然后分∠CEF=∠B和∠CEF=∠A两种情况,根据相似三角形对应边成比例列式求解即可.
解答:设BE=x,则EC=8-x,
∵沿DE折叠点B落的AC边上的F处,
∴EF=CE=x,
∠CEF=∠B时,∵△ABC∽△FEC,
∴
 =
=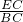 ,
,即
 =
=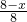 ,
,解得
 ,
,∠CEF=∠A时,∵△ABC∽△EFC,
∴
 =
=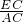 ,
,即
 =
= ,
,解得x=4,
综上所述,BE的长为
 或4.
或4.故答案为:
 或4.
或4.点评:本题考查了翻折变换的性质,相似三角形对应边成比例的性质,难点在于要分情况讨论.

练习册系列答案
相关题目
 如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论:①△BDF是等腰三角形;②DE=
如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论:①△BDF是等腰三角形;②DE= (2012•路南区一模)如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中一定正确的是( )
(2012•路南区一模)如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中一定正确的是( ) 如图,直角三角形纸片的两直角边AC=6cm,BC=8cm.现将直角边AC沿AD折叠,使它落在斜边AB上,点C与点E重合.求CD的长.
如图,直角三角形纸片的两直角边AC=6cm,BC=8cm.现将直角边AC沿AD折叠,使它落在斜边AB上,点C与点E重合.求CD的长. 如图,将三角形纸片ABC沿DE折叠,当点A落在四边形BDEC的外部时,∠1=72°,∠2=26°,则∠A=
如图,将三角形纸片ABC沿DE折叠,当点A落在四边形BDEC的外部时,∠1=72°,∠2=26°,则∠A=