Question

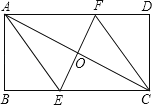
【题目】将矩形ABCD折叠使A，C重合，折痕交BC于E，交AD于F，

（1）求证：四边形AECF为菱形；

（2）若AB＝4，BC＝8，

①求菱形的边长；

②求折痕EF的长．

Answer 1

【答案】（1）见解析；（2）①5；②2．

【解析】

（1）根据折叠的性质得OA＝OC，EF⊥AC，EA＝EC，再利用AD∥AC得到∠FAC＝∠ECA，则可根据“ASA”判断△AOF≌△COE，得到OF＝OE，加上OA＝OC，AC⊥EF，于是可根据菱形的判定方法得到四边形AECF为菱形；

（2）①设菱形的边长为x，则BE＝BC﹣CE＝8﹣x，AE＝x，在Rt△ABE中，根据勾股定理得（8﹣x）2+42＝x2，然后解方程即可得到菱形的边长；

②先在Rt△ABC中，利用勾股定理计算出AC＝4，则OA＝AC＝2，然后在Rt△AOE中，利用勾股定理计算出OE＝，所以EF＝2OE＝2．

（1）∵矩形ABCD折叠使A，C重合，折痕为EF，

∴OA＝OC，EF⊥AC，EA＝EC，

∵AD∥AC，

∴∠FAC＝∠ECA，在△AOF和△COE中，

∴△AOF≌△COE，

∴OF＝OE，

∵OA＝OC，AC⊥EF，

∴四边形AECF为菱形；

（2）①设菱形的边长为x，则BE＝BC﹣CE＝8﹣x，AE＝x，

在Rt△ABE中，∵BE2+AB2＝AE2，

∴（8﹣x）2+42＝x2，解得x＝5，

即菱形的边长为5；

②在Rt△ABC中，AC＝＝4，

∴OA＝AC＝2，

在Rt△AOE中，AE＝5，

OE＝＝，

∴EF＝2OE＝2．