题目内容
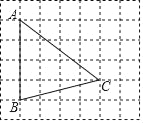
【题目】如图,在![]() 中,
中,![]() ,按以下步骤作图:
,按以下步骤作图:
①:以点![]() 为圆心,以小于
为圆心,以小于![]() 的长为半径画弧,分别交
的长为半径画弧,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ;
;
②:分别以点![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径画弧,两弧相交于点
的长为半径画弧,两弧相交于点![]() ;
;
③:作射线![]() ,交
,交![]() 边于点
边于点![]() ,
,
若![]() ,
,![]() ,则
,则![]() ( )
( )
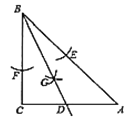
A. 3B. ![]() C. 6D.
C. 6D. ![]()
【答案】B
【解析】
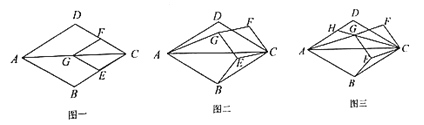
连接GF,EG,根据SSS定理可得出△BFG≌△BEG,故可得出∠GBF=∠GBE,即BD为∠ABC的平分线;根据勾股定理求出AC的长,过点D作DH⊥AB于点H,由角平分线的性质可得出CD=DH,再由三角形的面积公式即可得出CD的长,进而计算![]() .
.
连接GF,EG,

在△BFG与△BEG中,

∴△BFG≌△BEG(SSS),
∴∠GBF=∠GBE,即BD为∠ABC的平分线,
∵![]() ,
,![]() ,
,![]()
∴![]()
过点D作DH⊥AB于点H,
∵BD为∠ABC的平分线,
∴CD=DH,
∴![]()
∴![]() ,即
,即![]() 解得
解得![]() .
.
![]()
故选:B.

练习册系列答案
相关题目