题目内容
(1)如图1,P,Q,R是△ABC三边上的点,且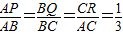 ,求
,求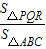 的值.
的值.在中学数学中,由2个数学系统中所含元素的属性在某些方面相同或相似,推出它们的其他属性也可能相同或相似的思维形式被称为类比推理,运用类比推理的模式解决数学问题的方法称为类比法.类比既是一种逻辑方法,也是一种科学研究的方法,是最重要的数学思想方法之一.
(2)请结合第一小题,完成下面小题的解答.如图2,E,F,G,H分别在四边形ABCD的四边上,且
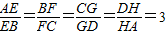 ,求
,求 的值.
的值.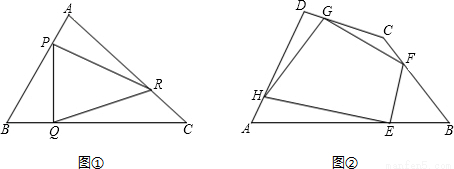
【答案】分析:(1)首先根据已知条件知AP= AB,BQ=
AB,BQ= BC,CR=
BC,CR= AC,BP=
AC,BP= AB,CQ=
AB,CQ= BC,AR=
BC,AR= AC;然后利用三角形的面积公式S=
AC;然后利用三角形的面积公式S= absinC求得△ABC中除去△PQR的三个小三角形的面积与△ABC的面积间的数量关系;最后由S△PQR=S△ABC-S△APR-S△BPQ-S△CQR=
absinC求得△ABC中除去△PQR的三个小三角形的面积与△ABC的面积间的数量关系;最后由S△PQR=S△ABC-S△APR-S△BPQ-S△CQR= S△ABC可以推知
S△ABC可以推知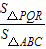 的值;
的值;
(2)连接BD、AC.解答过程同(1).
解答: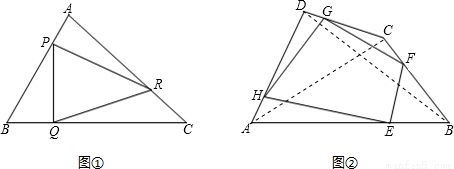 解:(1)∵P,Q,R是△ABC三边上的点,且
解:(1)∵P,Q,R是△ABC三边上的点,且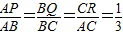 ,
,
∴AP= AB,BQ=
AB,BQ= BC,CR=
BC,CR= AC,
AC,
∴BP= AB,CQ=
AB,CQ= BC,AR=
BC,AR= AC,
AC,
∴S△APR= AP•ARsinA=
AP•ARsinA= ×
× AB•
AB• AC•sinA=
AC•sinA= ×
× AB•ACsinA=
AB•ACsinA= S△ABC;
S△ABC;
S△BPQ= BQ•BPsinB=
BQ•BPsinB= ×
× BC•
BC• AB•sinB=
AB•sinB= ×
× BC•ABsinB=
BC•ABsinB= S△ABC;
S△ABC;
S△CQR= CR•CQsinC=
CR•CQsinC= ×
× AC•
AC• BC•sinC=
BC•sinC= ×
× AC•BCsinC=
AC•BCsinC= S△ABC;
S△ABC;
∴S△PQR=S△ABC-S△APR-S△BPQ-S△CQR= S△ABC,
S△ABC,
∴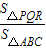 =
= ;
;
(2)连接BD、AC.
∵如图2,E,F,G,H分别在四边形ABCD的四边上,且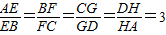 ,
,
∴AE= AB,AH=
AB,AH= AD,CF=
AD,CF= BC,CG=
BC,CG= CD,
CD,
∴S△AHE= AE•AHsin∠HAE=
AE•AHsin∠HAE= ×
× AB×
AB× ADsin∠HAE=
ADsin∠HAE=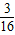 ×
× AB•ADsin∠HAE=
AB•ADsin∠HAE=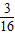 S△ABD,
S△ABD,
S△CFG= CF•CGsin∠DCB=
CF•CGsin∠DCB= ×
× CD×
CD× BCsin∠DCB=
BCsin∠DCB=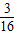 ×
× CD•BCsin∠DCB=
CD•BCsin∠DCB=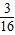 S△CDB,
S△CDB,
∴S△AHE+S△CFG=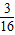 (S△ABD+S△CDB)=
(S△ABD+S△CDB)=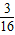 S四边形ABCD;
S四边形ABCD;
同理,S△DGH+S△BEF=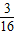 (S△ADC+S△ABC)=
(S△ADC+S△ABC)=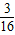 S四边形ABCD;
S四边形ABCD;
∴S四边形EFGH=S四边形ABCD-S△AHE-S△CFG-S△AHE-S△CFG= S四边形EFGH,
S四边形EFGH,
∴ =
= .
.
点评:本题考查了面积及等积转换.解答本题的关键是根据已知条件找出组成大图形中的小三角形的面积与大图形面积间的数量关系.
 AB,BQ=
AB,BQ= BC,CR=
BC,CR= AC,BP=
AC,BP= AB,CQ=
AB,CQ= BC,AR=
BC,AR= AC;然后利用三角形的面积公式S=
AC;然后利用三角形的面积公式S= absinC求得△ABC中除去△PQR的三个小三角形的面积与△ABC的面积间的数量关系;最后由S△PQR=S△ABC-S△APR-S△BPQ-S△CQR=
absinC求得△ABC中除去△PQR的三个小三角形的面积与△ABC的面积间的数量关系;最后由S△PQR=S△ABC-S△APR-S△BPQ-S△CQR= S△ABC可以推知
S△ABC可以推知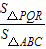 的值;
的值;(2)连接BD、AC.解答过程同(1).
解答:
 解:(1)∵P,Q,R是△ABC三边上的点,且
解:(1)∵P,Q,R是△ABC三边上的点,且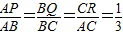 ,
,∴AP=
 AB,BQ=
AB,BQ= BC,CR=
BC,CR= AC,
AC,∴BP=
 AB,CQ=
AB,CQ= BC,AR=
BC,AR= AC,
AC,∴S△APR=
 AP•ARsinA=
AP•ARsinA= ×
× AB•
AB• AC•sinA=
AC•sinA= ×
× AB•ACsinA=
AB•ACsinA= S△ABC;
S△ABC;S△BPQ=
 BQ•BPsinB=
BQ•BPsinB= ×
× BC•
BC• AB•sinB=
AB•sinB= ×
× BC•ABsinB=
BC•ABsinB= S△ABC;
S△ABC;S△CQR=
 CR•CQsinC=
CR•CQsinC= ×
× AC•
AC• BC•sinC=
BC•sinC= ×
× AC•BCsinC=
AC•BCsinC= S△ABC;
S△ABC;∴S△PQR=S△ABC-S△APR-S△BPQ-S△CQR=
 S△ABC,
S△ABC,∴
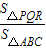 =
= ;
;(2)连接BD、AC.
∵如图2,E,F,G,H分别在四边形ABCD的四边上,且
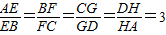 ,
,∴AE=
 AB,AH=
AB,AH= AD,CF=
AD,CF= BC,CG=
BC,CG= CD,
CD,∴S△AHE=
 AE•AHsin∠HAE=
AE•AHsin∠HAE= ×
× AB×
AB× ADsin∠HAE=
ADsin∠HAE=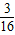 ×
× AB•ADsin∠HAE=
AB•ADsin∠HAE=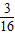 S△ABD,
S△ABD,S△CFG=
 CF•CGsin∠DCB=
CF•CGsin∠DCB= ×
× CD×
CD× BCsin∠DCB=
BCsin∠DCB=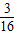 ×
× CD•BCsin∠DCB=
CD•BCsin∠DCB=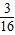 S△CDB,
S△CDB,∴S△AHE+S△CFG=
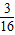 (S△ABD+S△CDB)=
(S△ABD+S△CDB)=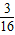 S四边形ABCD;
S四边形ABCD;同理,S△DGH+S△BEF=
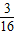 (S△ADC+S△ABC)=
(S△ADC+S△ABC)=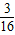 S四边形ABCD;
S四边形ABCD;∴S四边形EFGH=S四边形ABCD-S△AHE-S△CFG-S△AHE-S△CFG=
 S四边形EFGH,
S四边形EFGH,∴
 =
= .
.点评:本题考查了面积及等积转换.解答本题的关键是根据已知条件找出组成大图形中的小三角形的面积与大图形面积间的数量关系.

练习册系列答案
相关题目
 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB= 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.