题目内容
如图,每个小正方形的边长都是1,在每幅图中以格点为顶点,分别画出一个符合下列要求的三角形.
(1)三边长分别为3、
、5,并求此三角形的面积;
(2)边长是无理数的等腰直角三角形,并求此三角形的斜边长.

(1)三边长分别为3、
| 10 |
(2)边长是无理数的等腰直角三角形,并求此三角形的斜边长.

分析:(1)不妨在直接在一边上取3;以3和1为直角边则斜边为
;再以边长3和4为直角边为5斜边画三角形即可,根据所画图形和三角形的面积公式计算即可;
(2)可取任意相邻的两个正方形的对角线为直角边即
,再根据勾股定理即可求出斜边.
| 10 |
(2)可取任意相邻的两个正方形的对角线为直角边即
| 2 |
解答:解:(1)如图所示三角形ABC为所求,S△ABC=
AB•BC=
×3×3=
;

(2)如图所示:△DEF为所求,EF=
=2.

| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |

(2)如图所示:△DEF为所求,EF=
| DE2+DF2 |

点评:此题主要考查了勾股定理,应用与作图设计,关键要理解题意,弄清问题中对所作图形的要求,然后作图.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 23、如图,每个小正方形的边长为单位长度1.
23、如图,每个小正方形的边长为单位长度1.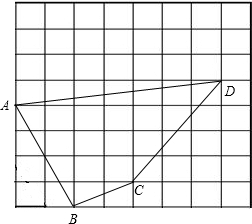 如图,每个小正方形的边长为1.
如图,每个小正方形的边长为1.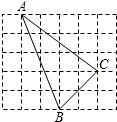 如图,每个小正方形的边长为1,则△ABC的面积等于
如图,每个小正方形的边长为1,则△ABC的面积等于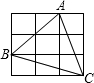 如图,每个小正方形的边长为1,以C为圆心3为半径的圆与AB的位置关系为
如图,每个小正方形的边长为1,以C为圆心3为半径的圆与AB的位置关系为 如图,每个小正方形的边长为1cm,蚂蚁从A点沿正方形的网格线,经过C点,爬到B点的最短路程是
如图,每个小正方形的边长为1cm,蚂蚁从A点沿正方形的网格线,经过C点,爬到B点的最短路程是