题目内容
【题目】直线![]() 与反比例函数
与反比例函数![]() 的图像分别交于点
的图像分别交于点![]() 和点
和点![]() ,与坐标轴分别交于点
,与坐标轴分别交于点![]() 和点
和点![]() .若点
.若点![]() 是
是![]() 轴上一动点,当
轴上一动点,当![]() 与
与![]() 相似时,则点
相似时,则点![]() 的坐标为______.
的坐标为______.
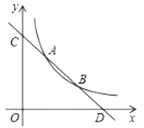
【答案】![]() 或
或![]()
【解析】
将A、B坐标代入反比例函数解析式求出m、n,然后将A、B坐标代入一次函数解析式,求出k,b,进而得到直线解析式,再求出C、D坐标,分别讨论两种情况,利用相似比建立方程求解.
解:∵![]() 和点
和点![]() 在反比例函数
在反比例函数![]() 上,
上,
∴![]() ,
,![]() ,
,
解得![]() ,
,
∴![]() ,
,![]()
把![]() ,
,![]() 代入直线
代入直线![]() ,得:
,得:
![]() ,解得
,解得![]() ,
,
∴直线![]()
当x=0时,![]() ,当
,当![]() 时,x=6,
时,x=6,
∴C点坐标(0,6),D点坐标(6,0)
∴OC=6,OD=6,
设P点坐标(a,0)
当△COD∽△APD时,如下图所示,
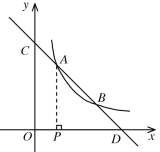
∵AP⊥x轴,
∴P点横坐标与A点相同,即a=2,
∴P点坐标为(2,0),
当△COD∽△PAD时,如下图所示,
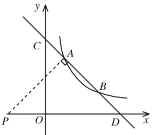
![]() ,
,![]()
∵△COD∽△PAD
∵![]()
∴![]()
解得![]() ,所以P点坐标为(-2,0)
,所以P点坐标为(-2,0)
综上,P点坐标为![]() 或
或![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】参照学习函数的过程方法,探究函数![]() 的图像与性质,因为
的图像与性质,因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究列表:
来探究列表:
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … | |
| … |
|
| 1 | 2 | 4 | -4 | -2 | -1 | <> |
| … | |
| … |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| … |
描点:在平面直角坐标系中以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点如图所示:
相应的函数值为纵坐标,描出相应的点如图所示:
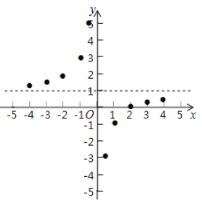
(1)请把![]() 轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而______;(“增大”或“减小”)
的增大而______;(“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向______平移______个单位而得到的;
的图象向______平移______个单位而得到的;
③图象关于点______中心对称.(填点的坐标)
(3)函数![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的面积.
的面积.