题目内容
【题目】已知四边形ABCD中,AD+DB+BC=16,则四边形ABCD的面积的最大值是( )
A. 16 B. 32 C. 16![]() D.
D. ![]()
【答案】B
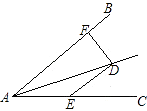
【解析】先画图,由于S四边形ABCD=S△ABD+S△BCD,那么当∠ADB=∠BCD=90°时,S△ABD、S△BCD有最大值,也就是四边形ABCD有最大值,再结合AD+DB+BC=16,可求S四边形ABCD=8BD-![]() BD2,再利用二次函数的求最值问题,即可求四边形ABCD的面积.
BD2,再利用二次函数的求最值问题,即可求四边形ABCD的面积.
解:如图所示,连接BD,
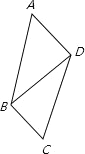
∵S四边形ABCD=S△ABD+S△BCD,
S△ABD=![]() ADBDsin∠ADB,
ADBDsin∠ADB,
S△BCD=![]() BDBCsin∠BCD,
BDBCsin∠BCD,
∴当∠ADB=∠BCD=90°时,S△ABD、S△BCD有最大值,
∴S四边形ABCD=S△ABD+S△BCD=![]() ADBD+
ADBD+![]() BDBC,
BDBC,
又∵AD+BC=16-BD,
∴S四边形ABCD=![]() BD(16-BD)=8BD-
BD(16-BD)=8BD-![]() BD2,
BD2,
∵a=-![]() <0,
<0,
∴当BD=-![]() =8时,四边形ABCD的面积有最大值=
=8时,四边形ABCD的面积有最大值=![]() =32.
=32.
故四边形ABCD的最大面积是32.
“点睛”本题考查了四边形面积的计算、二次函数的性质.已知两边和夹角,可利用夹角的正弦来求面积.要使三角形面积最大,则夹角应等于90°.

练习册系列答案
相关题目