Question

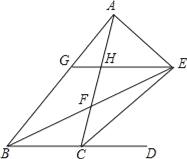
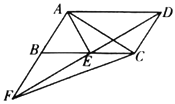
【题目】如图，在平行四边形中，平分，交于点，且，延长与的延长线交于点，连接，连接．下列结论中：①；②是等边角形：③；④；⑤.其中正确的是（ ）

A.②③⑤B.①④⑤C.①②③D.①②④

Answer 1

【答案】D

【解析】

由平行四边形的性质得出AD∥BC，AD＝BC，由AE平分∠BAD，可得∠BAE＝∠DAE，可得∠BAE＝∠BEA，得AB＝BE，由AB＝AE，得到△ABE是等边三角形，②正确；则∠ABE＝∠EAD＝60°，由SAS证明△ABC≌△EAD，①正确；由△CDF与△ABC等底（AB＝CD）等高（AB与CD间的距离相等），得出，④正确；由△AEC与△DCE同底等高，得出，进而得出．⑤不正确．

解：∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∴∠EAD＝∠AEB，
又∵AE平分∠BAD，
∴∠BAE＝∠DAE，
∴∠BAE＝∠BEA，
∴AB＝BE，
∵AB＝AE，
∴△ABE是等边三角形，②正确；
∴∠ABE＝∠EAD＝60°，
∵AB＝AE，BC＝AD，
∴△ABC≌△EAD（SAS），①正确；
∵△CDF与△ABC等底（AB＝CD）等高（AB与CD间的距离相等），
∴，④正确；
又∵△AEC与△DEC同底等高，
∴，
∴，⑤不正确．
若AD与AF相等，即∠AFD＝∠ADF＝∠DEC，题中未限定这一条件，
∴③不一定正确；
故正确的为：①②④．

故选：D．