题目内容
在Rt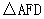 中,∠F="90°,点B、C分别在AD、FD上,以AB为直径的半圆O" 过点C,
中,∠F="90°,点B、C分别在AD、FD上,以AB为直径的半圆O" 过点C,
联结AC,将△AFC 沿AC翻折得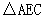 ,
, 且点E恰好落在直径AB上.
且点E恰好落在直径AB上.
(1)判断:直线FC与半圆O的位置关系是________ _____
_____ __;并证明你的结论.
__;并证明你的结论.
(2)若OB="BD=2,求CE的长." 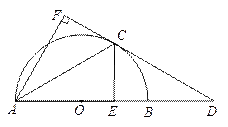
( 1)直线FC与⊙O的位置关系是_相切_;…
1)直线FC与⊙O的位置关系是_相切_;… ……………1’
……………1’
证明:联结OC
∵OA=OC,∴∠1=∠2,由翻折得,∠1=∠3,∠F=∠AEC=90°
∴∠3="∠2 " ……………………………………………………2’
∴OC∥AF,∴∠F="∠OCD=90°,∴FC与⊙O相切 " …………3’
(2)在Rt△OCD中,cos∠COD=
∴∠COD="60° " …………………………4’
在R t△OCD中,C
t△OCD中,C E=OC
E=OC ·sin∠COD=
·sin∠COD= ………………………5’
………………………5’
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
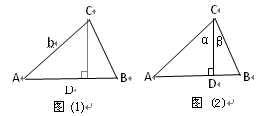
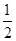 AC·BC·sin(α+β)=
AC·BC·sin(α+β)= 中,
中, ,
, ,则
,则 .
. 中,
中, ,点D是斜边AB上的一点,且CD=AC=3,AB=4,求
,点D是斜边AB上的一点,且CD=AC=3,AB=4,求 ,
, 及
及 的值.
的值.
 中,∠C=90°,AB=5,BC=3,则
中,∠C=90°,AB=5,BC=3,则 的值为( ).
的值为( ). B.
B. C.
C. D.
D.
 中,
中, ,点
,点 在
在 上,
上, ,
, ,
,
 ,求
,求 的长.
的长.