题目内容
【题目】在平面直角坐标系中,已知抛物线![]() 的顶点M的坐标为(﹣1,﹣4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
的顶点M的坐标为(﹣1,﹣4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
(1)填空:b= ,c= ,直线AC的解析式为 ;
(2)直线x=t与x轴相交于点H.
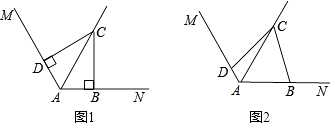
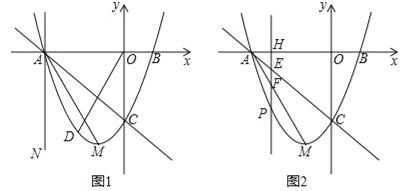
①当t=﹣3时得到直线AN(如图1),点D为直线AC下方抛物线上一点,若∠COD=∠MAN,求出此时点D的坐标;
②当﹣3<t<﹣1时(如图2),直线x=t与线段AC,AM和抛物线分别相交于点E,F,P.试证明线段HE,EF,FP总能组成等腰三角形;如果此等腰三角形底角的余弦值为![]() ,求此时t的值.
,求此时t的值.
【答案】(1)2,﹣3,y=﹣x﹣3;(2)①D(![]() ,
,![]() );②t=
);②t=![]() .
.
【解析】
试题分析:(1)根据顶点坐标列出关于b、c的方程组求解可得,由抛物线解析式求得A、C坐标,利用待定系数法可得直线AC解析式;
(2)①设点D的坐标为(m,![]() ),由∠COD=∠MAN得tan∠COD=tan∠MAN,列出关于m的方程求解可得;②求出直线AM的解析式,进而可用含t的式子表示出HE、EF、FP的长度,根据等腰三角形定义即可判定;由等腰三角形底角的余弦值为
),由∠COD=∠MAN得tan∠COD=tan∠MAN,列出关于m的方程求解可得;②求出直线AM的解析式,进而可用含t的式子表示出HE、EF、FP的长度,根据等腰三角形定义即可判定;由等腰三角形底角的余弦值为![]() 可得
可得![]() =
=![]() ,列方程可求得t的值.
,列方程可求得t的值.
试题解析:(1)∵抛物线![]() 的顶点M的坐标为(﹣1,﹣4),∴
的顶点M的坐标为(﹣1,﹣4),∴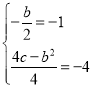 ,解得:
,解得:![]() ,∴抛物线解析式为:
,∴抛物线解析式为:![]() ,令y=0,得:
,令y=0,得:![]() ,解得:
,解得:![]() ,
,![]() ,∴A(﹣3,0),B(1,0),令x=0,得y=﹣3,∴C(0,﹣3),设直线AC的解析式为:y=kx+b,将A(﹣3,0),C(0,﹣3)代入,得:
,∴A(﹣3,0),B(1,0),令x=0,得y=﹣3,∴C(0,﹣3),设直线AC的解析式为:y=kx+b,将A(﹣3,0),C(0,﹣3)代入,得:![]() ,解得:
,解得:![]() ,∴直线AC的解析式为:y=﹣x﹣3;故答案为:2,﹣3,y=﹣x﹣3.
,∴直线AC的解析式为:y=﹣x﹣3;故答案为:2,﹣3,y=﹣x﹣3.
(2)①设点D的坐标为(m,![]() ),∵∠COD=∠MAN,∴tan∠COD=tan∠MAN,∴
),∵∠COD=∠MAN,∴tan∠COD=tan∠MAN,∴![]() ,解得:m=
,解得:m=![]() ,∵﹣3<m<0,∴m=
,∵﹣3<m<0,∴m=![]() ,故点D的坐标为(
,故点D的坐标为(![]() ,
,![]() );
);
②设直线AM的解析式为y=mx+n,将点A(﹣3,0)、M(﹣1,﹣4)代入,得:![]() ,解得:
,解得:![]() ,∴直线AM的解析式为:y=﹣2x﹣6,∵当x=t时,HE=﹣(﹣t﹣3)=t+3,HF=﹣(﹣2t﹣6)=2t+6,HP=
,∴直线AM的解析式为:y=﹣2x﹣6,∵当x=t时,HE=﹣(﹣t﹣3)=t+3,HF=﹣(﹣2t﹣6)=2t+6,HP=![]() ,∴HE=EF=HF﹣HE=t+3,FP=
,∴HE=EF=HF﹣HE=t+3,FP=![]() ,∵HE+EF﹣FP=
,∵HE+EF﹣FP=![]() =
=![]() >0,∴HE+EF>FP,又HE+FP>EF,EF+FP>HE,∴当﹣3<t<﹣1时,线段HE,EF,FP总能组成等腰三角形;
>0,∴HE+EF>FP,又HE+FP>EF,EF+FP>HE,∴当﹣3<t<﹣1时,线段HE,EF,FP总能组成等腰三角形;
由题意得:![]() =
=![]() ,即
,即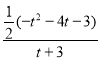 =
=![]() ,整理得:
,整理得:![]() ,解得:
,解得:![]() ,
, ![]() ,∵﹣3<t<﹣1,∴t=
,∵﹣3<t<﹣1,∴t=![]() .
.