题目内容
如图，某房地产开发公司购得一块三角形地块，在靠近∠B的内部有一千年的古樟树要加以保护，市政府规定要过P点划一三角形的保护区，你怎样划这条线才能使被划去的△BDE的面积最小？为什么？分析：过P作直线GF∥AB，交BC于G，交AC于F，在BC上取点E，使GE=BG，延长EP交AB于点D，则△BDE的面积最小．
先过P任作一直线，交BC于M，交AB于N，比较△BDE的面积和△BMN的面积，也就是比较△PME和△NDP的面积，由于GP∥AB，BG=GE，根据平行线分线段成比例定理易得DP=PE，再结合DK∥BC，易证△MPF≌△KPG，从而易知S△NPG＞S△MPF，进而可知S△BMN＞S△BFG，也就说明△BDE的面积最小．
先过P任作一直线，交BC于M，交AB于N，比较△BDE的面积和△BMN的面积，也就是比较△PME和△NDP的面积，由于GP∥AB，BG=GE，根据平行线分线段成比例定理易得DP=PE，再结合DK∥BC，易证△MPF≌△KPG，从而易知S△NPG＞S△MPF，进而可知S△BMN＞S△BFG，也就说明△BDE的面积最小．
解答：
解：过P作直线GF∥AB，交BC于G，交AC于F，在BC上取点E，
使GE=BG，延长EP交AB于点D，则△BDE的面积最小．
若过P任作一直线，交BC于M，交AB于N，
过D作DK∥BC，交MN于K，
∵GP∥AB，BG=GE，
∴DP：PE=BG：GE，
∴PD=PE，
又∵DK∥BC，
∴∠KDP=∠MEP，∠PKD=∠PME，
∴△MPF≌△KPG，
∴S△NPG＞S△MPF，
∴S△BMN＞S△BFG，
∴△BDE的面积最小．
解：过P作直线GF∥AB，交BC于G，交AC于F，在BC上取点E，使GE=BG，延长EP交AB于点D，则△BDE的面积最小．
若过P任作一直线，交BC于M，交AB于N，
过D作DK∥BC，交MN于K，
∵GP∥AB，BG=GE，
∴DP：PE=BG：GE，
∴PD=PE，
又∵DK∥BC，
∴∠KDP=∠MEP，∠PKD=∠PME，
∴△MPF≌△KPG，
∴S△NPG＞S△MPF，
∴S△BMN＞S△BFG，
∴△BDE的面积最小．
点评：本题考查了全等三角形的判定和性质、三角形中位线定理、平行线的性质、平行线分线段成比例定理，解题的关键是作辅助线，并进行比较．
练习册系列答案
相关题目
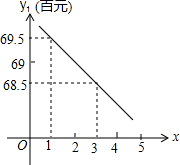（2013•邵东县模拟）重庆市某房地产开发公司在2012年2月以来销售商品房时，市场营销部经分析发现：随着国家政策调控措施的持续影响，大多市民持币观望态度浓厚，从2月起第1周到第五周，房价y1（百元/m2）与周数x（1≤x≤5，且x取正整数）之间存在如图所示的变化趋势：3月中旬由于房屋刚性需求的释放，出现房地产市场“小阳春”行情，房价逆市上扬，从第6周到第12周，房价y2与周数x（6≤x≤12，且x取整数）之间关系如下表：
如图，某房地产开发公司购得一块三角形地块，在靠近∠B的内部有一千年的古樟树要加以保护，市政府规定要过P点划一三角形的保护区，你怎样划这条线才能使被划去的△BDE的面积最小？为什么？
