题目内容
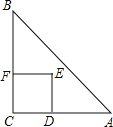
【题目】(8分)如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,C、D两点不重合,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,
(1)求y与x之间的函数关系
(2)x为何值时重叠部分的面积最大
【答案】(1) (2)2
(2)2
【解析】试题分析:(1)分类讨论:当0<x≤1时,根据正方形的面积公式得到y=x2;当1<x≤2时,ED交AB于M,EF交AB于N,利用重叠的面积等于正方形的面积减去等腰直角三角形MNE的面积得到y=x2-2(x-1)2,配方得到y=-(x-2)2+2;
(2)当0<x≤1时,y=x2,的最大值是1,当1<x≤2时,y=-(x-2)2+2的最大值是2,综合得当x=2时,y有最大值为2.
试题解析:(1)当0<x≤1时,y=x2,当1<x≤2时,ED交AB于M,EF交AB于N,如图,

CD=x,则AD=2﹣x,
∵Rt△ABC中,AC=BC=2,
∴△ADM为等腰直角三角形,
∴DM=2﹣x,∴EM=x﹣(2﹣x)=2x﹣2,
∴S△ENM=![]() (2x﹣2)2=2(x﹣1)2,
(2x﹣2)2=2(x﹣1)2,
∴y=x2﹣2(x﹣1)2=﹣x2+4x﹣2=﹣(x﹣2)2+2,
∴ ;
;
(2) ,
,
当0<x≤1时,y=x2,的最大值是1,当1<x≤2时,y=-(x-2)2+2的最大值是2,综合得当x=2时,y有最大值为2.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
