题目内容
(1)计算: ;
;
(2)解方程组: ;
;
(3)用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案:

根据规律填空:
①第4个图案中有白色地面砖______块;
②第n个图案中有白色地面砖______块.
解:(1)原式=1+5=6;
(2)把y=x+1代入x+y=5,得2x+1=5
∴x=2
∴y=2+1=3
∴原方程组的解为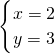 ;
;
(3)①从图中白砖与黑砖的块数找规律.我们可以发现,黑砖的数量是1,2,3,4,…,白砖的数量是6,10,14…,所以从第二块砖起,我们可以看出黑砖与白砖的数量关系是白=6n-2(n-1),其中n是黑砖的数量.所以第4个图案中有白色地面砖=18;
②第n个图案中有白色地面砖4n+2.
分析:(1)利用任何数的0次幂是1,进行有理数的运算即可;
(2)用加减法,先把y的系数转化成相同的或相反的数,然后两式相加减消元,从而求出x的值,然后把x的值代入一方程求y的值.
(3)主要是找规律,从图中白砖与黑砖的块数找规律.我们可以发现,黑砖的数量是1,2,3,4,…,白砖的数量是6,10,14…,所以从第二块砖起,我们可以看出黑砖与白砖的数量关系是白=6n-2(n-1),其中n是黑砖的数量.
点评:(1)题考查了实数的运算.(2)考查了解二元一次方程的能力.(3)题主要考查学生找规律的能力.
(2)把y=x+1代入x+y=5,得2x+1=5
∴x=2
∴y=2+1=3
∴原方程组的解为
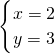 ;
;(3)①从图中白砖与黑砖的块数找规律.我们可以发现,黑砖的数量是1,2,3,4,…,白砖的数量是6,10,14…,所以从第二块砖起,我们可以看出黑砖与白砖的数量关系是白=6n-2(n-1),其中n是黑砖的数量.所以第4个图案中有白色地面砖=18;
②第n个图案中有白色地面砖4n+2.
分析:(1)利用任何数的0次幂是1,进行有理数的运算即可;
(2)用加减法,先把y的系数转化成相同的或相反的数,然后两式相加减消元,从而求出x的值,然后把x的值代入一方程求y的值.
(3)主要是找规律,从图中白砖与黑砖的块数找规律.我们可以发现,黑砖的数量是1,2,3,4,…,白砖的数量是6,10,14…,所以从第二块砖起,我们可以看出黑砖与白砖的数量关系是白=6n-2(n-1),其中n是黑砖的数量.
点评:(1)题考查了实数的运算.(2)考查了解二元一次方程的能力.(3)题主要考查学生找规律的能力.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
