题目内容
抛物线y=x2+2x-1与x轴交于A、B,点P是抛物线上的点,且S△PAB=2
,则满足条件的P点有
| 2 |
3
3
个.分析:先根据抛物线的对称轴=-2求出其顶点坐标,令y=0求出抛物线与x轴的交点坐标,再求出AB的长度,设出P点坐标,利用三角形的面积求出x的值.
解答:解:∵抛物线的对称轴=-2,
∴抛物线的顶点坐标为(-2,-1),
令y=0,则x2+2x-1=0,解得x1=-1-
,x2=-1+
,
∴AB=-1-
-(-1+
)=2
,
∵抛物线的顶点坐标为(-2,-1),
∴当点P在抛物线的顶点时△PAB的面积为2
;
∵抛物线开口向上,
∴除顶点坐标外另外符合条件的点一定在y轴的正半轴,
设P点坐标为(x,x2+2x-1),则
AB(x2+2x-1)=2
,
∴
×2
×(x2+2x-1)=2
,解得x=1或x=-3,即除顶点坐标外另外符合条件的点有两个,
∴符合条件的点有3个.
故答案为:3.
∴抛物线的顶点坐标为(-2,-1),
令y=0,则x2+2x-1=0,解得x1=-1-
| 2 |
| 2 |
∴AB=-1-
| 2 |
| 2 |
| 2 |
∵抛物线的顶点坐标为(-2,-1),
∴当点P在抛物线的顶点时△PAB的面积为2
| 2 |
∵抛物线开口向上,
∴除顶点坐标外另外符合条件的点一定在y轴的正半轴,
设P点坐标为(x,x2+2x-1),则
| 1 |
| 2 |
| 2 |
∴
| 1 |
| 2 |
| 2 |
| 2 |
∴符合条件的点有3个.
故答案为:3.
点评:本题考查的是抛物线与x轴的交点问题及三角形的面积公式,在解答此题时一定要先判断出当点P在抛物线的顶点时是否符合条件,这是此题的易错点.

练习册系列答案
相关题目
抛物线y=x2+2x-2的图象上最低点的坐标是( )
| A、(2,-2) | B、(1,-2) | C、(1,-3) | D、(-1,-3) |
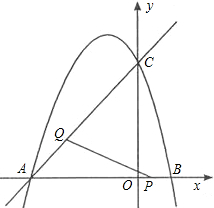 秒,请求出△APQ的面积S与t的函数关系式,并求出当t为何值时,△APQ的面积最大,最大面积是多少?
秒,请求出△APQ的面积S与t的函数关系式,并求出当t为何值时,△APQ的面积最大,最大面积是多少?