题目内容
两个全等的三角形ABC和DEF重叠在一起,△ABC的面积为3,且AB=CB,固定△ABC不动,将△DEF进行如下操作:
(1)如图①,△DEF沿线段AB向右平移(即D点在线段AB内移动),连接DC、CF、FB,四边形CDBF的形状在不断地变化,但它的面积不变化,请求出其面积;
(2)如图②,当D点B向右平移到B点时,试判断CE与BF的位置关系,并说明理由;
(3)在(2)的条件下,若∠AEC=15°,求AB的长.
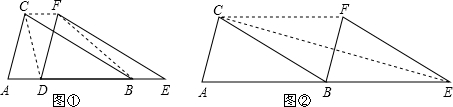
(1)如图①,△DEF沿线段AB向右平移(即D点在线段AB内移动),连接DC、CF、FB,四边形CDBF的形状在不断地变化,但它的面积不变化,请求出其面积;
(2)如图②,当D点B向右平移到B点时,试判断CE与BF的位置关系,并说明理由;
(3)在(2)的条件下,若∠AEC=15°,求AB的长.

分析:(1)首先过点C作CE⊥AB于点H,由平移的性质可得:CF=AD,CF∥AB,即可得S四边形CDBF=
(CF+BD)•CH=
(AD+BD)•CH=
AB•CH=S△ABC=3;
(2)由平移的性质可得:BE=CF,BE∥CF,可证得四边形CBEF是平行四边形;又由AB=BC=BE,即可得?CBEF是菱形,由菱形的性质可证得:CE⊥BF;
(3)首先过点C作CG⊥AB于点G,由∠AEC=15°,可得∠ABC=30°,即可得CG=
CB=
AB,又由△ABC的面积为3,即可求得AB的长.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由平移的性质可得:BE=CF,BE∥CF,可证得四边形CBEF是平行四边形;又由AB=BC=BE,即可得?CBEF是菱形,由菱形的性质可证得:CE⊥BF;
(3)首先过点C作CG⊥AB于点G,由∠AEC=15°,可得∠ABC=30°,即可得CG=
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:(1)过点C作CE⊥AB于点H,
解:(1)过点C作CE⊥AB于点H,
由平移的性质可得:CF=AD,CF∥AB,
∴S四边形CDBF=
(CF+BD)•CH=
(AD+BD)•CH=
AB•CH,
∵S△ABC=
AB•CH=3,
∴S四边形CDBF=3;
(2)CE⊥BF.
理由:由平移的性质可得:BE=CF,BE∥CF,
∴四边形CBEF是平行四边形,
∵AB=CB,AB=BE,
∴CB=BE,
∴?CBEF是菱形,
∴CE⊥BF;
(3)过点C作CG⊥AB于点G,
∵CB=BE,∠AEC=15°,
∴∠BCE=∠AEC=15°,
∴∠ABC=∠AEC+∠BCE=30°,
∴在Rt△BCG中,CG=
CB,
∵AB=CB,
∴CG=
AB,
∴S△ABC=
AB•CG=
AB2=3,
解得:AB=2
.
 解:(1)过点C作CE⊥AB于点H,
解:(1)过点C作CE⊥AB于点H,由平移的性质可得:CF=AD,CF∥AB,
∴S四边形CDBF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ABC=
| 1 |
| 2 |
∴S四边形CDBF=3;
(2)CE⊥BF.
理由:由平移的性质可得:BE=CF,BE∥CF,
∴四边形CBEF是平行四边形,
∵AB=CB,AB=BE,
∴CB=BE,
∴?CBEF是菱形,
∴CE⊥BF;
(3)过点C作CG⊥AB于点G,
∵CB=BE,∠AEC=15°,
∴∠BCE=∠AEC=15°,
∴∠ABC=∠AEC+∠BCE=30°,
∴在Rt△BCG中,CG=
| 1 |
| 2 |
∵AB=CB,
∴CG=
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 4 |
解得:AB=2
| 3 |
点评:此题考查了菱形的判定与性质、等腰三角形的性质以及含30°角的直角三角形的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
 11、如图所示,四边形ABCD是平行四边形,那么下列说法正确的有( )
11、如图所示,四边形ABCD是平行四边形,那么下列说法正确的有( )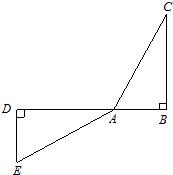 15、两个全等的三角形如下图所示放置,点B、A、D在同一直线上.操作:在图中,在CB边上截取CM=AB,连接DM,交AC于N.请探究∠AND的大小,并证明你的结论.
15、两个全等的三角形如下图所示放置,点B、A、D在同一直线上.操作:在图中,在CB边上截取CM=AB,连接DM,交AC于N.请探究∠AND的大小,并证明你的结论.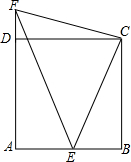 明理由;它们能够由其中一个通过旋转而得到另外一个吗?简述旋转过程.
明理由;它们能够由其中一个通过旋转而得到另外一个吗?简述旋转过程. 如图1,将等腰直角三角形纸片ABC沿底边上的高CD剪开,得到两个全等的三角形△ADC,△BDC,已知AC=4.
如图1,将等腰直角三角形纸片ABC沿底边上的高CD剪开,得到两个全等的三角形△ADC,△BDC,已知AC=4.