题目内容
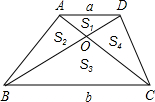 如图,梯形ABCD,对角线AC与BD相交于O,设AD=a,BC=b,△AOD,△AOB,△BOC,△COD的面积分别为S1、S2、S3、S4,则下列各式中错误的是( )
如图,梯形ABCD,对角线AC与BD相交于O,设AD=a,BC=b,△AOD,△AOB,△BOC,△COD的面积分别为S1、S2、S3、S4,则下列各式中错误的是( )A、
| ||||
B、
| ||||
C、
| ||||
| D、S1+S3=S2+S4 |
分析:相似三角形的面积比等于对应边长的平方比,依此可判定A,B,C的正确性,D中面积的和只可能成比例,并不相等
解答:解:∵AD∥BC,
∴△AOD∽△COB,
∴
=
,
∴A正确;
同理,∵△AOD∽△COB,
∴
=
=
,
∵△AOD与△AOB等高,
∴S1:S2=AD:BC=a:b,B正确.
同理C也正确,
由B,C可知S1=
S2,S3=
S4,
∴S1+S3=
(S2+S4)
所以D错误.
故选D.

∴△AOD∽△COB,
∴
| S1 |
| S3 |
| a2 |
| b2 |
∴A正确;
同理,∵△AOD∽△COB,
∴
| OD |
| OB |
| OA |
| OC |
| a |
| b |
∵△AOD与△AOB等高,
∴S1:S2=AD:BC=a:b,B正确.
同理C也正确,
由B,C可知S1=
| a |
| b |
| b |
| a |
∴S1+S3=
| a2+b2 |
| ab |
所以D错误.
故选D.
点评:熟练掌握相似三角形的性质,能够利用相似三角形的性质求解一些线段的比例及面积之间的比例问题.

练习册系列答案
相关题目
 如图,梯形ABCD中,AB∥CD,E是AD中点,EF∥CB交AB于F,BC=4cm,则EF的长等于( )
如图,梯形ABCD中,AB∥CD,E是AD中点,EF∥CB交AB于F,BC=4cm,则EF的长等于( )| A、1.5cm | B、2cm | C、2.5cm | D、3cm |
 如图,梯形ABCD中,EF∥BC,AD=4,EF=5,BC=7,则DF:FC=
如图,梯形ABCD中,EF∥BC,AD=4,EF=5,BC=7,则DF:FC=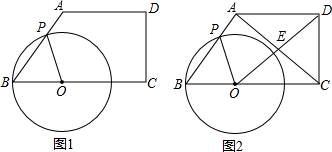
 如图,梯形ABCD内接于⊙O,AD∥BC,∠DAB=49°,则∠AOC的度数为
如图,梯形ABCD内接于⊙O,AD∥BC,∠DAB=49°,则∠AOC的度数为 如图,梯形ABCD中,DE∥AB交下底BC于E,AF∥CD交下底BC于F,且DE⊥AF,垂足为O.若AO=3cm,DO=4cm,四边形ABED的面积为36cm2,则梯形ABCD的周长为( )
如图,梯形ABCD中,DE∥AB交下底BC于E,AF∥CD交下底BC于F,且DE⊥AF,垂足为O.若AO=3cm,DO=4cm,四边形ABED的面积为36cm2,则梯形ABCD的周长为( )