题目内容
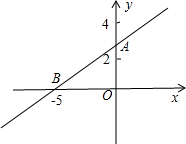 如图直线l与x轴、y轴分别交于点B、A两点,且A、B两点的坐标分别为A(0,3),B(-4,0).
如图直线l与x轴、y轴分别交于点B、A两点,且A、B两点的坐标分别为A(0,3),B(-4,0).(1)请求出直线l的函数解析式;
(2)点P在x轴上,且ABP是等腰三角形,请直接写出所有符合条件的点P的坐标;
(3)点C为直线AB上一个动点,是否存在使点C到x轴的距离为1.5?若存在,求出点C的坐标;若不存在,请说明理由.
分析:(1)设直线l的函数解析式是y=kx+b(k≠0),把满足条件的点的坐标代入,求出k、b即可;
(2)设P(x,0),则根据两点间的距离公式列方程,把A(0,3),B(-4,0)代入求值;
(3)假设存在使点C(x,1.5)到x轴的距离为1.5的点C存在,把该点代入(1)的函数解析式若适合,则存在;反之,不存在.
(2)设P(x,0),则根据两点间的距离公式列方程,把A(0,3),B(-4,0)代入求值;
(3)假设存在使点C(x,1.5)到x轴的距离为1.5的点C存在,把该点代入(1)的函数解析式若适合,则存在;反之,不存在.
解答:解:(1)设y=kx+b(k≠0),(1分)
由题意,得
得
(3分)
∴y=0.75x+3.(4分)
(2)设P(x,0).
∵△ABP是等腰三角形,
∴①当|PA|=|PB|时,
=
,
解得x=-
,
∴P(-
,0);
②当|AB|=|AP|时,
=
,
解得x=±4,
∵P点与B点不重合,
∴P(4,0);
③当|AB|=|BP|时,
=
,
解得,
x=-9或x=1,
∴P(-9,0)或(1,0);
∴所有符合条件的点P的坐标是P1(-
,0),P2(4,0),P3(-9,0),P4(1,0).
(3)假设存在点C(x,±1.5)到x轴的距离为1.5,则点C(x,±1.5)满足方程y=0.75x+3,
①当C(x,1.5)时,
1.5=0.75x+3,解得x=-2,
∴点C(-2,1.5)存在;
②当C(x,-1.5)时,
-1.5=0.75x+3,解得x=-6,
所以C(-6,-1.5)存在.
∴存在点C(x,±1.5)到x轴的距离为1.5,其坐标是(-2,1.5)或(-6,-1.5).
由题意,得
|
|
∴y=0.75x+3.(4分)
(2)设P(x,0).
∵△ABP是等腰三角形,
∴①当|PA|=|PB|时,
| x2+9 |
| (x+4)2 |
解得x=-
| 7 |
| 8 |
∴P(-
| 7 |
| 8 |
②当|AB|=|AP|时,
| x2+9 |
| 16+9 |
解得x=±4,
∵P点与B点不重合,
∴P(4,0);
③当|AB|=|BP|时,
| (-4)2+32 |
| (x+4)2 |
解得,
x=-9或x=1,
∴P(-9,0)或(1,0);
∴所有符合条件的点P的坐标是P1(-
| 7 |
| 8 |
(3)假设存在点C(x,±1.5)到x轴的距离为1.5,则点C(x,±1.5)满足方程y=0.75x+3,
①当C(x,1.5)时,
1.5=0.75x+3,解得x=-2,
∴点C(-2,1.5)存在;
②当C(x,-1.5)时,
-1.5=0.75x+3,解得x=-6,
所以C(-6,-1.5)存在.
∴存在点C(x,±1.5)到x轴的距离为1.5,其坐标是(-2,1.5)或(-6,-1.5).
点评:(1)用待定系数法求一次函数解析式;
(2)分类讨论:|PA|=|PB|;|AB|=|AP|;|AB|=|BP|,不要漏解;
(3)正确理解直线上的点与直线方程是一一对应关系.
(2)分类讨论:|PA|=|PB|;|AB|=|AP|;|AB|=|BP|,不要漏解;
(3)正确理解直线上的点与直线方程是一一对应关系.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
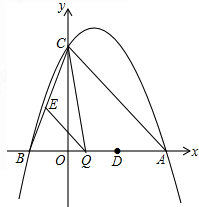 (2012•浦江县模拟)已知:如图,抛物线与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0),点B的坐标为(-2,0).
(2012•浦江县模拟)已知:如图,抛物线与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0),点B的坐标为(-2,0). BP交⊙P于点C
BP交⊙P于点C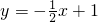 分别与x轴、y轴交于点A、B,在第一象限取点C,使△ABC成为等腰直角三角形;如果在第二象限内有一点P(a,
分别与x轴、y轴交于点A、B,在第一象限取点C,使△ABC成为等腰直角三角形;如果在第二象限内有一点P(a, ),使△ABP的面积与Rt△ABC的面积相等,求a的值.
),使△ABP的面积与Rt△ABC的面积相等,求a的值.
 如图直线l与x轴、y轴分别交于点B、A两点,且A、B两点的坐标分别为A(0,3),B(-4,0).
如图直线l与x轴、y轴分别交于点B、A两点,且A、B两点的坐标分别为A(0,3),B(-4,0).