题目内容
某班共有35名学生,其中一半男生和三分之一的女生骑自行车上学,那么该班骑自行车上学的学生的人数最少是
- A.9
- B.10
- C.11
- D.12
D
分析:设有a个男生骑车,b个女生骑车,则可得2a+3b=35,求a+b的最小值即可得出答案.
解答:设有a个男生骑车,b个女生骑车,则题目可简写成2a+3b=35,
解法①当b=1时,a=16;当b=2时,b=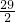 ;当b=3时,a=13;当b=4时,a=
;当b=3时,a=13;当b=4时,a= ;当b=5时,a=10;当b=6时,a=
;当b=5时,a=10;当b=6时,a= ;
;
当b=7时,a=7;当b=8时,a= ;当b=9时,a=4;当b=10时,a=
;当b=9时,a=4;当b=10时,a= ;当b=11时,a=1;
;当b=11时,a=1;
∵a、b均为正整数,
∴可得a+b的最小值为12,即该班骑自行车上学的学生的人数最少12人.
解法②∵2a+3b=35,
∴a= ,a+b=
,a+b= ,b≤11.
,b≤11.
故可得当b=11时,a+b的值最小,最小值为12.
故选D.
点评:此题考查了二元一次方程的应用,解答本题的关键是设出未知数,得出二元一次方程,根据a、b均为正整数进行解答.
分析:设有a个男生骑车,b个女生骑车,则可得2a+3b=35,求a+b的最小值即可得出答案.
解答:设有a个男生骑车,b个女生骑车,则题目可简写成2a+3b=35,
解法①当b=1时,a=16;当b=2时,b=
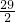 ;当b=3时,a=13;当b=4时,a=
;当b=3时,a=13;当b=4时,a= ;当b=5时,a=10;当b=6时,a=
;当b=5时,a=10;当b=6时,a= ;
;当b=7时,a=7;当b=8时,a=
 ;当b=9时,a=4;当b=10时,a=
;当b=9时,a=4;当b=10时,a= ;当b=11时,a=1;
;当b=11时,a=1;∵a、b均为正整数,
∴可得a+b的最小值为12,即该班骑自行车上学的学生的人数最少12人.
解法②∵2a+3b=35,
∴a=
 ,a+b=
,a+b= ,b≤11.
,b≤11.故可得当b=11时,a+b的值最小,最小值为12.
故选D.
点评:此题考查了二元一次方程的应用,解答本题的关键是设出未知数,得出二元一次方程,根据a、b均为正整数进行解答.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
“慈善一日捐”这天,某校师生积极捐款,根据捐款结果,绘制出八年级(1)班50名同学捐款(捐款额为整数)的频数分布表:
请结合图表,完成下列问题:
(1)表中的a= ;
(2)这个样本数据的中位数落在 组;
(3)捐款数为20.5~30.5元这组的频率是多少?
(4)该校八年级共有学生400名,捐款额不低于20元的八年级学生大约多少名?
| 组别/元 | 组中值/元 | 频数/人数 |
| 0.5~10.5 | 5.5 | 18 |
| 10.5~20.5 | 15.5 | 16 |
| 20.5~30.5 | 25.5 | 8 |
| 30.5~40.5 | 35.5 | a |
| 40.5~50.5 | 45.5 | 2 |
(1)表中的a=
(2)这个样本数据的中位数落在
(3)捐款数为20.5~30.5元这组的频率是多少?
(4)该校八年级共有学生400名,捐款额不低于20元的八年级学生大约多少名?