题目内容
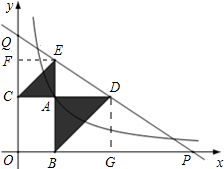
 (2012•温州)如图,已知动点A在函数y=
(2012•温州)如图,已知动点A在函数y=| 4 |
| x |
| 13 |
| 3 |
| 13 |
| 3 |
分析:过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.令A(t,
),则AD=AB=DG=
,AE=AC=EF=t,则图中阴影部分的面积=△ACE的面积+△ABD的面积=
t2+
×
,因此只需求出t2的值即可.先在直角△ADE中,由勾股定理,得出DE=
,再由△EFQ∽△DAE,求出QE=
,△ADE∽△GPD,求出DP=:
,然后根据QE:DP=4:9,即可得出t2=
.
| 4 |
| t |
| 4 |
| t |
| 1 |
| 2 |
| 1 |
| 2 |
| 16 |
| t2 |
| ||
| t |
t
| ||
| 4 |
4
| ||
| t3 |
| 8 |
| 3 |
解答:解:解法一:过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.
令A(t,
),则AD=AB=DG=
,AE=AC=EF=t.
在直角△ADE中,由勾股定理,得DE=
=
=
=
.
∵△EFQ∽△DAE,
∴QE:DE=EF:AD,
∴QE=
,
∵△ADE∽△GPD,
∴DE:PD=AE:DG,
∴DP=
.
又∵QE:DP=4:9,
∴=
:
=4:9,
解得t2=
.
∴图中阴影部分的面积=
AC2+
AB2=
t2+
×
=
+3=
;
解法二:∵QE:DP=4:9,
∴EF:PG=4:9,
设EF=4t,则PG=9t,
∴A(4t,
),
由AC=AE AD=AB,
∴AE=4t,AD=
,DG=
,GP=9t,
∵△ADE∽△GPD,
∴AE:DG=AD:GP,
4t:
=
:9t,即t2=
,
图中阴影部分的面积=
×4t×4t+
×
×
=
.
故答案为:
.
令A(t,
| 4 |
| t |
| 4 |
| t |
在直角△ADE中,由勾股定理,得DE=
| AD2+AE2 |
|
|
| ||
| t |
∵△EFQ∽△DAE,
∴QE:DE=EF:AD,
∴QE=
t
| ||
| 4 |

∵△ADE∽△GPD,
∴DE:PD=AE:DG,
∴DP=
4
| ||
| t3 |
又∵QE:DP=4:9,
∴=
t
| ||
| 4 |
4
| ||
| t3 |
解得t2=
| 8 |
| 3 |
∴图中阴影部分的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 16 |
| t2 |
| 4 |
| 3 |
| 13 |
| 3 |
解法二:∵QE:DP=4:9,
∴EF:PG=4:9,
设EF=4t,则PG=9t,
∴A(4t,
| 1 |
| t |
由AC=AE AD=AB,
∴AE=4t,AD=
| 1 |
| t |
| 1 |
| t |
∵△ADE∽△GPD,
∴AE:DG=AD:GP,
4t:
| 1 |
| t |
| 1 |
| t |
| 1 |
| 6 |
图中阴影部分的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| t |
| 1 |
| t |
| 13 |
| 3 |
故答案为:
| 13 |
| 3 |
点评:本题考查了反比例函数的性质,勾股定理,相似三角形的判定与性质,三角形的面积等知识,综合性较强,有一定难度.根据QE:DP=4:9,得出t2的值是解题的关键.

练习册系列答案
相关题目
 (2012•温州)如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连接CB,CP.
(2012•温州)如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连接CB,CP. (2012•温州)如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
(2012•温州)如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.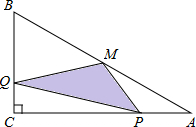 (2012•温州)如图,在△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
(2012•温州)如图,在△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )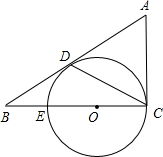 (2012•温州)如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(2012•温州)如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.