题目内容
17.计算:1+2+1=4
1+2+3+2+1=9
1+2+3+4+3+2+1=16
1+2+3+4+5+4+3+2+1=25
根据上面四式的计算规律求:1+2+3+4+…+2004+2005+2004+…+4+3+2+1=4020025.
分析 因为1+2+1=4=22,1+2+3+2+1=9=32,1+2+3+4+3+2+1=16=42,1+2+3+4+5+4+3+2+1=25=52,…由此得出1+2+3+…+n+…+3+2+1=n2;据此解答.
解答 解:∵1+2+1=4=22,
1+2+3+2+1=9=32,
1+2+3+4+3+2+1=16=42,
1+2+3+4+5+4+3+2+1=25=52,
…
∴1+2+3+…+n+…+3+2+1=n2;
∴1+2+3+4+…+2004+2005+2004+…+4+3+2+1=20052=4020025.
故答案为:4,9,16,25,4020025.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
2.下列各对数值,不是二元一次方程2x+y=6的解的是( )
| A. | $\left\{\begin{array}{l}x=0\\ y=6\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=\frac{1}{2}\\ y=5\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=-2\\ y=-10\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=3\\ y=0\end{array}\right.$ |
7.下列各对数中互为相反数的是( )
| A. | -(+5)和+(-5) | B. | -(-5)和+(-5) | C. | -(+5)和-5 | D. | +(-5)和-5 |
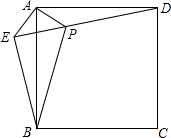 如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=2.
如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=2.