ЬтФПФкШн
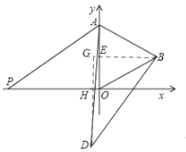
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЁїAOBЪЧЕШБпШ§НЧаЮЃЌЕуAЕФзјБъЪЧЃЈ0ЃЌ4ЃЉЃЌЕуBдкЕквЛЯѓЯоЃЌЕуPЪЧxжсЩЯЕФвЛИіЖЏЕуЃЌСЌНгAPЃЌВЂАбЁїAOPШЦзХЕуAАДФцЪБеыЗНЯђа§зЊЃЌЪЙБпAOгыABжиКЯЃЌЕУЕНЁїABDЃЎ

ЃЈ1ЃЉЧѓжБЯпABЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБЕуPдЫЖЏЕНЕуЃЈ![]() ЃЌ0ЃЉЪБЃЌЧѓДЫЪБDPЕФГЄМАЕуDЕФзјБъЃЛ
ЃЌ0ЃЉЪБЃЌЧѓДЫЪБDPЕФГЄМАЕуDЕФзјБъЃЛ
ЃЈ3ЃЉЪЧЗёДцдкЕуPЃЌЪЙЁїOPDЕФУцЛ§ЕШгк![]() ЃПШєДцдкЃЌЧыЧѓГіЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧыЧѓГіЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПНтЃКЃЈ1ЃЉШчД№ЭМ1ЃЌЙ§ЕуBзїBEЁЭyжсгкЕуEЃЌзїBFЁЭxжсгкЕуFЁЃ
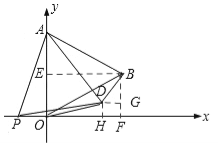
гЩвбжЊЕУЃКBF=OE=2ЃЌЁр![]() ЁЃ
ЁЃ
ЁрЕуBЕФзјБъЪЧЃЈ![]() ЃЌ2ЃЉЁЃ
ЃЌ2ЃЉЁЃ
ЩшжБЯпABЕФНтЮіЪНЪЧy=kx+bЃЈkЁй0ЃЉЃЌдђга
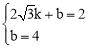 ЃЌНтЕУ
ЃЌНтЕУ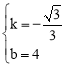 ЁЃ
ЁЃ
ЁржБЯпABЕФНтЮіЪНЪЧ![]() ЁЃ
ЁЃ
ЃЈ2ЃЉЁпЁїABDгЩЁїAOPа§зЊЕУЕНЃЌ
ЁрЁїABDЁеЁїAOPЁЃЁрAP=ADЃЌЁЯDAB=ЁЯPAOЁЃ
ЁрЁЯDAP=ЁЯBAO=60ЁуЁЃЁрЁїADPЪЧЕШБпШ§НЧаЮЁЃ
Ёр![]() ЁЃ
ЁЃ
ШчД№ЭМ2ЃЌЙ§ЕуDзїDHЁЭxжсгкЕуHЃЌбгГЄEBНЛDHгкЕуGЃЌдђBGЁЭDHЁЃ
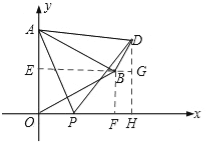
дкRtЁїBDGжаЃЌЁЯBGD=90ЁуЃЌЁЯDBG=60ЁуЃЌ
ЁрBG=BDcos60Ёу=![]() ЃЎDG=BDsin60Ёу=
ЃЎDG=BDsin60Ёу=![]() ЁЃ
ЁЃ
ЁрOH=EG=![]() ЃЌDH=
ЃЌDH=![]() ЁЃ
ЁЃ
ЁрЕуDЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЁЃ
ЃЉЁЃ
ЃЈ3ЃЉДцдкЁЃ
МйЩшДцдкЕуPЃЌдкЫќЕФдЫЖЏЙ§ГЬжаЃЌЪЙЁїOPDЕФУцЛ§ЕШгк![]() ЁЃ
ЁЃ
ЩшЕуPЮЊЃЈtЃЌ0ЃЉЃЌЯТУцЗжШ§жжЧщПіЬжТлЃК
ЂйЕБtЃО0ЪБЃЌШчД№ЭМ2ЃЌBD=OP=tЃЌDG=![]() tЃЌЁрDH=2+
tЃЌЁрDH=2+![]() tЁЃ
tЁЃ
ЁпЁїOPDЕФУцЛ§ЕШгк![]() ЃЌЁр
ЃЌЁр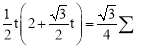 ЃЌ
ЃЌ
НтЕУ![]() ЃЈЩсШЅЃЉЁЃ
ЃЈЩсШЅЃЉЁЃ
ЁрЕуP1ЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉЁЃ
ЃЌ0ЃЉЁЃ
ЂкЁпЕБDдкxжсЩЯЪБЃЌШчД№ЭМ3ЃЌ

ИљОнШёНЧШ§НЧКЏЪ§ЧѓГіBD=OP=![]() ЃЌ
ЃЌ
ЁрЕБ![]() ЃМtЁм0ЪБЃЌШчД№ЭМ1ЃЌBD=OP=ЉtЃЌDG=
ЃМtЁм0ЪБЃЌШчД№ЭМ1ЃЌBD=OP=ЉtЃЌDG=![]() tЃЌ
tЃЌ
ЁрGH=BF=2ЉЃЈ![]() tЃЉ=2+
tЃЉ=2+![]() tЁЃ
tЁЃ
ЁпЁїOPDЕФУцЛ§ЕШгк![]() ЃЌЁр
ЃЌЁр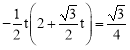 ЃЌНтЕУ
ЃЌНтЕУ![]() ЁЃ
ЁЃ
ЁрЕуP2ЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉЃЌЕуP3ЕФзјБъЮЊЃЈ
ЃЌ0ЃЉЃЌЕуP3ЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉЁЃ
ЃЌ0ЃЉЁЃ
ЂлЕБtЁм![]() ЪБЃЌШчД№ЭМ4ЃЌBD=OP=ЉtЃЌDG=
ЪБЃЌШчД№ЭМ4ЃЌBD=OP=ЉtЃЌDG=![]() tЃЌ
tЃЌ
ЁрDH=![]() tЉ2ЁЃ
tЉ2ЁЃ
ЁпЁїOPDЕФУцЛ§ЕШгк![]() ЃЌ
ЃЌ
Ёр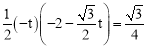 ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЈЩсШЅЃЉЁЃ
ЃЈЩсШЅЃЉЁЃ
ЁрЕуP4ЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉЁЃ
ЃЌ0ЃЉЁЃ
злЩЯЫљЪіЃЌЕуPЕФзјБъЗжБ№ЮЊP1ЃЈ![]() ЃЌ0ЃЉЁЂP2ЃЈ
ЃЌ0ЃЉЁЂP2ЃЈ![]() ЃЌ0ЃЉЁЂP3ЃЈ
ЃЌ0ЃЉЁЂP3ЃЈ![]() ЃЌ0ЃЉЁЂ
ЃЌ0ЃЉЁЂ
P4ЃЈ![]() ЃЌ0ЃЉЁЃ
ЃЌ0ЃЉЁЃ
ЁОНтЮіЁПЃЈ1ЃЉЙ§ЕуBзїBEЁЭyжсгкЕуEЃЌзїBFЁЭxжсгкЕуFЃЎвРЬтвтЕУBF=OE=2ЃЌРћгУЙДЙЩЖЈРэЧѓГіOFЃЌШЛКѓПЩЕУЕуBЕФзјБъЃЎЩшжБЯпABЕФНтЮіЪНЪЧy=kx+bЃЌАбвбжЊзјБъДњШыПЩЧѓНтЁЃ
ЃЈ2ЃЉгЩЁїABDгЩЁїAOPа§зЊЕУЕНЃЌЁїABDЁеЁїAOPЃЌAP=ADЃЌЁЯDAB=ЁЯPAOЃЌЁЯDAP=ЁЯBAO=60ЁуЃЌЁїADPЪЧЕШБпШ§НЧаЮЃЌРћгУЙДЙЩЖЈРэЧѓГіDPЃЎдкRtЁїBDGжаЃЌЁЯBGD=90ЁуЃЌЁЯDBG=60ЁуЃЎРћгУШ§НЧКЏЪ§ЧѓГіBG=BDcos60ЁуЃЌDG=BDsin60ЁуЃЎШЛКѓЧѓГіOHЃЌDHЃЌШЛКѓЧѓГіЕуDЕФзјБъЁЃ
ЃЈ3ЃЉЗжШ§жжЧщПіНјааЬжТлЃК
ЂйЕБPдкxжсе§АыжсЩЯЪБЃЌМДtЃО0ЪБЃЛ
ЂкЕБPдкxжсИКАыжсЃЌЕЋDдкxжсЩЯЗНЪБЃЛМД![]() ЃМtЁм0ЪБ
ЃМtЁм0ЪБ
ЂлЕБPдкxжсИКАыжсЃЌDдкxжсЯТЗНЪБЃЌМДtЁм![]() ЪБЁЃ
ЪБЁЃ
злКЯЩЯУцШ§жжЧщПіМДПЩЧѓГіЗћКЯЬѕМўЕФtЕФжЕЁЃ

 аТЗЧЗВНЬИЈГхДЬ100ЗжЯЕСаД№АИ
аТЗЧЗВНЬИЈГхДЬ100ЗжЯЕСаД№АИЁОЬтФПЁПЮЪЬтЃКЬНОПКЏЪ§y=|x|Љ2ЕФЭМЯѓгыаджЪЃЎ
аЁЛЊИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§y=|x|Љ2ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁЛЊЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉдкКЏЪ§y=|x|Љ2жаЃЌздБфСПxПЩвдЪЧШЮвтЪЕЪ§ЃЛ
ЃЈ2ЃЉШчБэЪЧyгыxЕФМИзщЖдгІжЕЃЎ
x | Ё | Љ3 | Љ2 | Љ1 | 0 | 1 | 2 | 3 | Ё |
y | Ё | 1 | 0 | Љ1 | Љ2 | Љ1 | 0 | m | Ё |
Ђйm=ЁЁ ЁЁЃЛ
ЂкШєAЃЈnЃЌ8ЃЉЃЌBЃЈ10ЃЌ8ЃЉЮЊИУКЏЪ§ЭМЯѓЩЯВЛЭЌЕФСНЕуЃЌдђn=ЁЁ ЁЁЃЛ
ЃЈ3ЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌУшГівдЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЎВЂИљОнУшГіЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
ИљОнКЏЪ§ЭМЯѓПЩЕУЃК
ЂйИУКЏЪ§ЕФзюаЁжЕЮЊЁЁ ЁЁЃЛ
ЂквбжЊжБЯп![]() гыКЏЪ§y=|x|Љ2ЕФЭМЯѓНЛгкCЁЂDСНЕуЃЌЕБy1ЁнyЪБxЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЎ
гыКЏЪ§y=|x|Љ2ЕФЭМЯѓНЛгкCЁЂDСНЕуЃЌЕБy1ЁнyЪБxЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЎ





