Question

【题目】如图，以△ABC的边AC为直径的⊙O恰为△ABC的外接圆，∠ABC的平分线交⊙O于点D，过点D作DE∥AC交BC的延长线于点E．

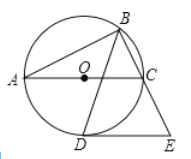
(1)若∠BAC＝28°20′，则∠E＝ ；

(2)求证：DE是⊙O的切线；

(3)若tan∠ACB＝2 ，BC＝2，求DE的长．

Answer 1

【答案】（1）；（2）详见解析；（3）7.5

【解析】

（1）根据直径所对圆周角是直角和平行线的性质，即可得解；

（2）根据圆周角定理和切线的判定方法，可得出DE是⊙O的切线；

（3）根据题意可首先求出半径，然后过点作，垂足为，易得四边形为正方形，进而得出tan∠CEG=tan∠BCA，即，由此可求出答案．

（1）∵AC是⊙O的直径

∴∠BAC+∠BCA=90°

∴

又∵DE∥AC

∴∠E=∠BCA=

故答案为：；

（2）证明：连接，

是⊙的直径，

平分

是⊙的切线；

（3）在中，∵tan∠ACB＝2，，

∴，

过点作，垂足为，则四边形为正方形，

∴