Question

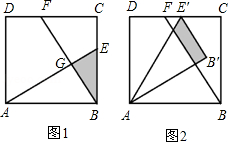
已知：如图1，在面积为3的正方形ABCD中，E、F分别是BC和CD边上的两点，AE⊥BF于点G，且BE=1．

（1）求证：△ABE≌△BCF；

（2）求出△ABE和△BCF重叠部分（即△BEG）的面积；

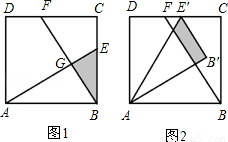
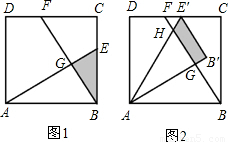
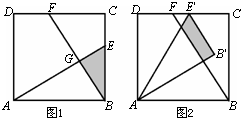
（3）现将△ABE绕点A逆时针方向旋转到△AB＇E＇（如图2），使点E落在CD边

上的点E＇处，问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化？请说明理由．

 

Answer 1

⑴证明：∵正方形ABCD中，∠ABE=∠BCF=90⁰ ，AB=BC，

            ∴∠ABF+∠CBF=90⁰，

             ∵AE⊥BF，

             ∴∠ABF+∠BAE=90⁰，

             ∴∠BAE=∠CBF，

             ∴△ABE≌△BCF.

⑵解：∵正方形面积为3，∴AB=，  

在△BGE与△ABE中， ∵∠GBE=∠BAE, ∠EGB=∠EBA=90⁰

            ∴△BGE∽△ABE           

        ∴，又BE=1，∴AE²=AB²+BE²=3+1=4

            ∴==.  

(用其他方法解答仿上步骤给分).

⑶解：没有变化 ∵AB=，BE=1，∴tan∠BAE=,∠BAE=30°,

∵AB′=AD，∠AB′E′=∠ADE＇=90°,AE′公共，

∴Rt△ABE≌Rt△AB′E′≌Rt△ADE′,

∴∠DAE′=∠B′AE′=∠BAE=30°,

∴AB′与AE在同一直线上，即BF与AB′的交点是G，

设BF与AE′的交点为H,

则∠BAG=∠HAG=30°,而∠AGB=∠AGH=90°,AG公共，

∴△BAG≌△HAG,

∴=== .

∴△ABE在旋转前后与△BCF重叠部分的面积没有变化.