ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦ,“―÷Σ≈ΉΈοœΏΨ≠ΙΐΒψ![]() ,
,![]() ,
,![]() »ΐΒψ,Βψ
»ΐΒψ,Βψ![]() ”κΒψ
”κΒψ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ÷αΕ‘≥Τ,Βψ
÷αΕ‘≥Τ,Βψ![]() «œΏΕΈ
«œΏΕΈ![]() …œΒΡ“ΜΗωΕ·Βψ,…ηΒψ
…œΒΡ“ΜΗωΕ·Βψ,…ηΒψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() ,ΙΐΒψ
,ΙΐΒψ![]() Ής
Ής![]() ÷αΒΡ¥ΙœΏΫΜ≈ΉΈοœΏ”ΎΒψ
÷αΒΡ¥ΙœΏΫΜ≈ΉΈοœΏ”ΎΒψ![]() ,ΫΜ÷±œΏ
,ΫΜ÷±œΏ![]() ”ΎΒψ
”ΎΒψ![]() .
.
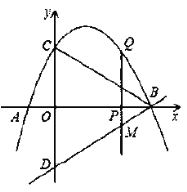
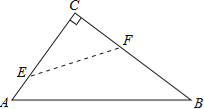
(1)«σΗΟ≈ΉΈοœΏΥυ±μ ΨΒΡΕΰ¥ΈΚ· ΐΒΡ±μ¥ο Ϋ;
(2)‘ΎΒψ![]() ‘ΥΕ·Ιΐ≥Χ÷–, «Ζώ¥φ‘ΎΒψ
‘ΥΕ·Ιΐ≥Χ÷–, «Ζώ¥φ‘ΎΒψ![]() , ΙΒΟ“‘
, ΙΒΟ“‘![]() ΈΣ÷±ΨΕΒΡ‘≤”κ
ΈΣ÷±ΨΕΒΡ‘≤”κ![]() ÷αœύ«–?»τ¥φ‘Ύ,«σ≥ω
÷αœύ«–?»τ¥φ‘Ύ,«σ≥ω![]() ΒΡ÷Β;»τ≤Μ¥φ‘Ύ,«κΥΒΟςάμ”…;
ΒΡ÷Β;»τ≤Μ¥φ‘Ύ,«κΥΒΟςάμ”…;
(3)Ν§Ϋ”![]() ,ΫΪ
,ΫΪ![]() »ΤΤΫΟφΡΎΡ≥Βψ
»ΤΤΫΟφΡΎΡ≥Βψ![]() Υ≥ ±’κ–ΐΉΣ
Υ≥ ±’κ–ΐΉΣ![]() ,ΒΟΒΫ
,ΒΟΒΫ![]() ,Βψ
,Βψ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΒΡΕ‘”ΠΒψΖ÷±π «Βψ
ΒΡΕ‘”ΠΒψΖ÷±π «Βψ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() .»τ
.»τ![]() ΒΡΝΫΗωΕΞΒψ«ΓΚΟ¬δ‘Ύ≈ΉΈοœΏ…œ,Ρ«Ο¥Έ“Ο«ΨΆ≥Τ’β―υΒΡΒψ
ΒΡΝΫΗωΕΞΒψ«ΓΚΟ¬δ‘Ύ≈ΉΈοœΏ…œ,Ρ«Ο¥Έ“Ο«ΨΆ≥Τ’β―υΒΡΒψ![]() ΈΣΓΑΚΆ–≥ΒψΓ±, Ρ«Ο¥Έ“Ο«ΨΆ≥Τ’β―υΒΡΒψΈΣΓΑΚΆ–≥ΒψΓ±Θ§«κ÷±Ϋ”–¥≥ωΓΑΚΆ–≥ΒψΓ±ΒΡΗω ΐΚΆΒψA1ΒΡΚαΉχ±ξ.
ΈΣΓΑΚΆ–≥ΒψΓ±, Ρ«Ο¥Έ“Ο«ΨΆ≥Τ’β―υΒΡΒψΈΣΓΑΚΆ–≥ΒψΓ±Θ§«κ÷±Ϋ”–¥≥ωΓΑΚΆ–≥ΒψΓ±ΒΡΗω ΐΚΆΒψA1ΒΡΚαΉχ±ξ.
ΓΨ¥πΑΗΓΩ(1)![]() ΘΜ(2)
ΘΜ(2)![]() ΘΜ(3)2ΗωΘΜA1ΚαΉχ±ξΈΣ1Μρ
ΘΜ(3)2ΗωΘΜA1ΚαΉχ±ξΈΣ1Μρ![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©Α―ΒψAΘ®1Θ§0Θ©ΓΔBΘ®4Θ§0Θ©ΓΔCΘ®0Θ§3Θ©»ΐΒψΒΡΉχ±ξ¥ζ»κΚ· ΐΫβΈω ΫΘ§άϊ”Ο¥ΐΕ®œΒ ΐΖ®«σΫβΘΜ
Θ®2Θ©œ»«σ≥ωBD÷±œΏΫβΈω ΫΘ§ΗυΨίΧβ“βΒΟΒΫ2OP=QM=÷±ΨΕdΦ¥Ω…«σΫβΘΜ
Θ®3Θ©ΝΫΗωΚΆ–≥ΒψΘΜAOΘΫ1Θ§OCΘΫ2Θ§…ηA1Θ®xΘ§yΘ©Θ§‘ρC1Θ®xΘΪ2Θ§y1Θ©Θ§O1Θ®xΘ§y1Θ©Θ§ΔΌΒ±A1ΓΔC1‘Ύ≈ΉΈοœΏ…œ ±Θ§ΔΎΒ±O1ΓΔC1‘Ύ≈ΉΈοœΏ…œΖ÷±π¥ζ»κ«σΫβ.
Θ®1Θ©…η≈ΉΈοœΏΫβΈω ΫΈΣyΘΫax2ΘΪbxΘΪcΘ§
ΫΪΒψAΘ®1Θ§0Θ©Θ§BΘ®4Θ§0Θ©Θ§CΘ®0Θ§2Θ©¥ζ»κΫβΈω ΫΘ§
Γύ Θ§
Θ§
ΫβΒΟ Θ§
Θ§
Γύ![]() ΘΜ
ΘΜ
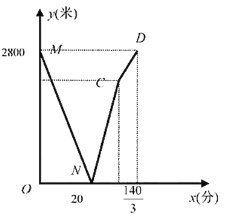
Θ®2Θ©ΓΏΒψC”κΒψDΙΊ”Ύx÷αΕ‘≥ΤΘ§
ΓύDΘ®0Θ§2Θ©Θ°
…η÷±œΏBDΒΡΫβΈω ΫΈΣyΘΫkx2Θ°
ΓΏΫΪΘ®4Θ§0Θ©¥ζ»κΒΟΘΚ4k2ΘΫ0Θ§
ΓύkΘΫ![]() Θ°
Θ°
Γύ÷±œΏBDΒΡΫβΈω ΫΈΣyΘΫ![]() x2Θ°
x2Θ°
Β±Βψ![]() , ΙΒΟ“‘
, ΙΒΟ“‘![]() ΈΣ÷±ΨΕΒΡ‘≤”κ
ΈΣ÷±ΨΕΒΡ‘≤”κ![]() ÷αœύ«–Θ§
÷αœύ«–Θ§
Γύ2OP=QM= d
ΓΏP![]()
ΓύQΘ®m,![]() Θ©,M(m,
Θ©,M(m, ![]() m2)
m2)
Ι 2m=Θ®![]() Θ©-Θ®
Θ©-Θ®![]() m2Θ©
m2Θ©
ΫβΒΟm=2Μρm=-4,
ΓΏΒψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§Ι m=-4≤ΜΖϊΚœΧβ“βΘ§
…œΘ§Ι m=-4≤ΜΖϊΚœΧβ“βΘ§
Ι m=2ΘΜ
Θ®3Θ©ΝΫΗωΚΆ–≥ΒψΘΜ
ΓΏAOΘΫ1Θ§OCΘΫ2Θ§
…ηA1Θ®xΘ§yΘ©Θ§‘ρC1Θ®xΘΪ2Θ§y1Θ©Θ§O1Θ®xΘ§y1Θ©Θ§
ΓύΔΌΒ±A1ΓΔC1‘Ύ≈ΉΈοœΏ…œ ±Θ§

Γύ
Γύ![]() Θ§
Θ§
ΓύA1ΒΡΚαΉχ±ξ «1ΘΜ
ΔΎΒ±O1ΓΔC1‘Ύ≈ΉΈοœΏ…œ ±Θ§

 Θ§
Θ§
Γύ
ΓύA1ΒΡΚαΉχ±ξ «![]() .
.

 ΆθΚσ–έ―ßΑΗΫΧ≤ΡΆξ»ΪΫβΕΝœΒΝ–¥πΑΗ
ΆθΚσ–έ―ßΑΗΫΧ≤ΡΆξ»ΪΫβΕΝœΒΝ–¥πΑΗ