题目内容
四边形ABCD中,AC、BD交于点O,则下列条件能判断四边形是正方形的有
①AC⊥BD,AO=CO=BO=DO;②AB=CD=AD=BC,AC=BD;③AO=BO=CO=DO;④∠A=90°,AB=AD;⑤AB∥CD,AB=BC=CD.
- A.2个
- B.3个
- C.4个
- D.5个
A
分析:根据正方形的性质与判定,对角线互相垂直的矩形是正方形,对角线相等的菱形是正方形,以及矩形判定,菱形判定逐个选项进行判断即可得出答案.
解答: 解:①AC⊥BD,AO=CO=BO=DO;
解:①AC⊥BD,AO=CO=BO=DO;
当AO=CO=BO=DO;可判定四边形ABCD是矩形,再利用AC⊥BD能判定它是正方形,故此选项正确;
②AB=CD=AD=BC,AC=BD;
由AB=CD=AD=BC可判定四边形ABCD是菱形,再利用AC=BD能判定它是正方形,故此选项正确;
③AO=BO=CO=DO;
当AO=CO=BO=DO;可判定四边形ABCD是矩形,不能判定它是正方形,故此选项错误;
④∠A=90°,AB=AD;
无法确定此四边形的形状,故此选项错误;
⑤AB∥CD,AB=BC=CD.
由AB∥CD,AB=CD可得出四边形ABCD是平行四边形,再利用AB=BC故此四边形是菱形,故此选项错误.
故正确的有2个,
故选:A.
点评:此题主要考查了正方形的判定以及菱形、矩形的判定,熟练掌握其性质与判定是解题关键.
分析:根据正方形的性质与判定,对角线互相垂直的矩形是正方形,对角线相等的菱形是正方形,以及矩形判定,菱形判定逐个选项进行判断即可得出答案.
解答:
 解:①AC⊥BD,AO=CO=BO=DO;
解:①AC⊥BD,AO=CO=BO=DO;当AO=CO=BO=DO;可判定四边形ABCD是矩形,再利用AC⊥BD能判定它是正方形,故此选项正确;
②AB=CD=AD=BC,AC=BD;
由AB=CD=AD=BC可判定四边形ABCD是菱形,再利用AC=BD能判定它是正方形,故此选项正确;
③AO=BO=CO=DO;
当AO=CO=BO=DO;可判定四边形ABCD是矩形,不能判定它是正方形,故此选项错误;
④∠A=90°,AB=AD;
无法确定此四边形的形状,故此选项错误;
⑤AB∥CD,AB=BC=CD.
由AB∥CD,AB=CD可得出四边形ABCD是平行四边形,再利用AB=BC故此四边形是菱形,故此选项错误.
故正确的有2个,
故选:A.
点评:此题主要考查了正方形的判定以及菱形、矩形的判定,熟练掌握其性质与判定是解题关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.
23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.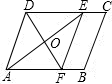 如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( )
如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( ) 17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形:
17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形: 7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.
7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.