题目内容
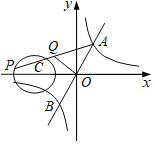
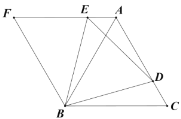
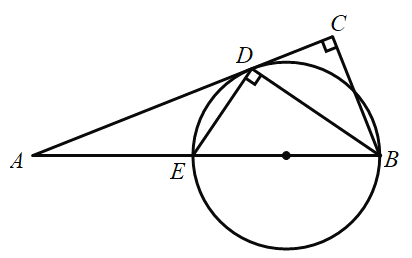
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,作
,作![]() 的外接圆.
的外接圆.
(1)判断直线![]() 与
与![]() 外接圆的位置关系,并说明理由;
外接圆的位置关系,并说明理由;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)直线![]() 与
与![]() 外接圆相切.理由见解析;(2)
外接圆相切.理由见解析;(2)![]()
【解析】
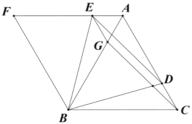
(1)可先观察图,猜想位置关系为相切,而要证明相切,需证得垂直,故取BD的中点O,联结OE后,结合两半径构成的等腰三角形性质和角平分线定义,易证得确为垂直关系;
(2)由(1)的结论,根据相似三角形的判定方法证明![]() ,进而根据相似三角形的性质结合正切值再求出
,进而根据相似三角形的性质结合正切值再求出![]() ,
,![]() ,然后推出
,然后推出![]() ,由相似三角形的性质即可求出求
,由相似三角形的性质即可求出求![]() 的长.
的长.
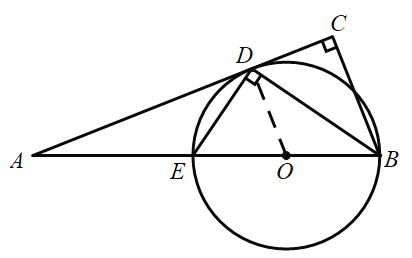
解:(1)直线![]() 与
与![]() 外接圆相切.
外接圆相切.
理由:∵![]() .
.
∴![]() 为
为![]() 外接圆的直径,
外接圆的直径,
取![]() 中点
中点![]() ,连结
,连结![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]()
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
又∵点![]() 在
在![]() 上
上
∴直线![]() 与
与![]() 外接圆相切.
外接圆相切.
(2)∵![]() ,
,
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
又![]()
∴![]()
∴![]() ,即
,即![]()
解得![]() ,
,![]()
![]()
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴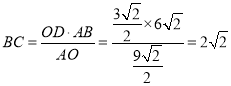

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目