题目内容
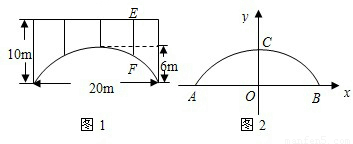
 (1)一辆宽2m的货车要通过跨度为8m、拱高为4m的单行抛物线隧道(从正中通过),为了保证安全,车顶离隧道顶部至少要0.5m的距离,货车的限高为多少?
(1)一辆宽2m的货车要通过跨度为8m、拱高为4m的单行抛物线隧道(从正中通过),为了保证安全,车顶离隧道顶部至少要0.5m的距离,货车的限高为多少?(2)若将(1)中的单行道改为双行道,即货车必须从隧道中线的右侧通过,货车的限高应是多少?
分析:(1)根据跨度求出点B的坐标,然后设抛物线顶点式形式y=ax2+4,然后把点B的坐标代入求出a的值,即可得解;
(2)根据车的宽度为2,求出x=1时的函数值,再根据限高求出可装货物的最大高度即可.
(2)根据车的宽度为2,求出x=1时的函数值,再根据限高求出可装货物的最大高度即可.
解答: 解:(1)∵隧道跨度为8米,隧道的顶端坐标为(O,4),
解:(1)∵隧道跨度为8米,隧道的顶端坐标为(O,4),
∴A、B关于y轴对称,
∴OA=OB=
AB=
×8=4,
∴点B的坐标为(4,0),
设抛物线顶点式形式y=ax2+4,
把点B坐标代入得,16a+4=0,
解得a=-
,
所以,抛物线解析式为y=-
x2+4(-4≤x≤4);
(2)∵车的宽度为2米,车从正中通过,
∴x=1时,y=-
×12+4=
,
∴货车安全行驶装货的最大高度为
-
=
(米).
当x=2时,y=3,
故货车限高为3-0.5=2.5(米).
 解:(1)∵隧道跨度为8米,隧道的顶端坐标为(O,4),
解:(1)∵隧道跨度为8米,隧道的顶端坐标为(O,4),∴A、B关于y轴对称,
∴OA=OB=
| 1 |
| 2 |
| 1 |
| 2 |
∴点B的坐标为(4,0),
设抛物线顶点式形式y=ax2+4,
把点B坐标代入得,16a+4=0,
解得a=-
| 1 |
| 4 |
所以,抛物线解析式为y=-
| 1 |
| 4 |
(2)∵车的宽度为2米,车从正中通过,
∴x=1时,y=-
| 1 |
| 4 |
| 15 |
| 4 |
∴货车安全行驶装货的最大高度为
| 15 |
| 4 |
| 1 |
| 2 |
| 13 |
| 4 |
当x=2时,y=3,
故货车限高为3-0.5=2.5(米).
点评:本题考查了二次函数的应用,主要利用了二次函数的图象的对称性,待定系数法求二次函数解析式,以及二次函数图象上点的坐标特征,比较简单.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
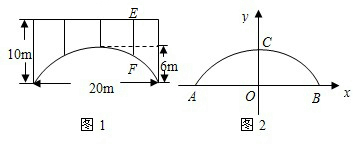
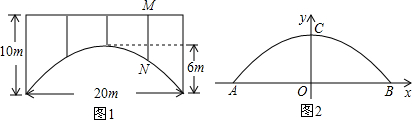
 (1)一辆宽2m的货车要通过跨度为8m、拱高为4m的单行抛物线隧道(从正中通过),为了保证安全,车顶离隧道顶部至少要0.5m的距离,货车的限高为多少?
(1)一辆宽2m的货车要通过跨度为8m、拱高为4m的单行抛物线隧道(从正中通过),为了保证安全,车顶离隧道顶部至少要0.5m的距离,货车的限高为多少?