题目内容
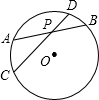
 如图,⊙O中的两弦AB⊥CD于E,已知BE-AE=6,⊙O的半径为5,则CD的长为
如图,⊙O中的两弦AB⊥CD于E,已知BE-AE=6,⊙O的半径为5,则CD的长为
- A.12
- B.10
- C.6
- D.8
D
分析:过O作OM⊥CD于M,OF⊥AB与F,连接OC,证四边形OMEF是矩形,推出OM=EF,根据垂径定理求出CD=2CM,求出EF,根据勾股定理求出CM即可.
解答: 解:过O作OM⊥CD于M,OF⊥AB与F,连接OC,
解:过O作OM⊥CD于M,OF⊥AB与F,连接OC,
∵OM⊥CD,OF⊥AB,AB⊥CD,
∴∠OME=∠OFE=∠MEF=90°,
∴四边形OMEF是矩形,
∴OM=EF,
∵OF⊥AB,OM⊥CD,
∴CD=2CM,AB=2AF=2BF,
∵BE-AE=6,
当BN=AE时,EF=FN,
∴EF=3=OM,
在△COM中,由勾股定理得:CM= =4,
=4,
∴CD=8.
故选D.
点评:本题主要考查对垂径定理,勾股定理,矩形的性质和判定等知识点的理解和掌握,能求出OM和CM的长是解此题的关键.
分析:过O作OM⊥CD于M,OF⊥AB与F,连接OC,证四边形OMEF是矩形,推出OM=EF,根据垂径定理求出CD=2CM,求出EF,根据勾股定理求出CM即可.
解答:
 解:过O作OM⊥CD于M,OF⊥AB与F,连接OC,
解:过O作OM⊥CD于M,OF⊥AB与F,连接OC,∵OM⊥CD,OF⊥AB,AB⊥CD,
∴∠OME=∠OFE=∠MEF=90°,
∴四边形OMEF是矩形,
∴OM=EF,
∵OF⊥AB,OM⊥CD,
∴CD=2CM,AB=2AF=2BF,
∵BE-AE=6,

当BN=AE时,EF=FN,
∴EF=3=OM,
在△COM中,由勾股定理得:CM=
 =4,
=4,∴CD=8.
故选D.
点评:本题主要考查对垂径定理,勾股定理,矩形的性质和判定等知识点的理解和掌握,能求出OM和CM的长是解此题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目