题目内容
【题目】如图的三角形纸片中,AB=AC,BC=12cm,∠C=30°,折叠这个三角形,使点B落在AC的中点D处,折痕为EF,那么BF的长为cm. 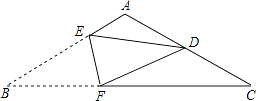
【答案】![]()
【解析】解:过D作DH⊥BC,过点A作AN⊥BC于点N, 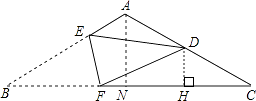
∵AB=AC,
∴∠B=∠C=30°,
根据折叠可得:DF=BF,∠EDF=∠B=30°,
∵AB=AC,BC=12cm,
∴BN=NC=6cm,
∵点B落在AC的中点D处,AN∥DH,
∴NH=HC=3cm,
∴DH=3tan30°= ![]() (cm),
(cm),
设BF=DF=xcm,则FH=12﹣x﹣3=9﹣x(cm),
故在Rt△DFC中,DF2=DH2+FH2 ,
故x2=( ![]() )2+(9﹣x)2 ,
)2+(9﹣x)2 ,
解得:x= ![]() ,
,
即BF的长为: ![]() cm.
cm.
故答案为: ![]() .
.
首先过D作DH⊥BC,过点A作AN⊥BC于点N,根据题意结合等腰三角形的性质进而得出CN的长,再利用锐角三角函数关系以及勾股定理得出答案.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目