题目内容
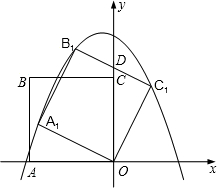 如图,正方形ABCO的边长为
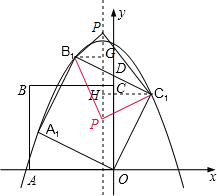
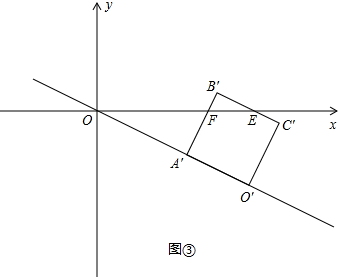
如图,正方形ABCO的边长为 ,以O为原点建立平面直角坐标系,点A在x轴的负半轴上,点C在y轴的正半轴上,把正方形ABCO绕点O顺时针旋转α后得到正方形A1B1C1O(α<45°),B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.
,以O为原点建立平面直角坐标系,点A在x轴的负半轴上,点C在y轴的正半轴上,把正方形ABCO绕点O顺时针旋转α后得到正方形A1B1C1O(α<45°),B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.
(1)填空:tanα=______;抛物线的函数表达式是______;
(2)在抛物线的对称轴上是否存在点P,使△PB1C1为直角三角形?若存在,直接写出所有满足条件的P点坐标;若不存在,请说明理由;
(3)若正方形A1B1C1O以每秒2 个单位长度的速度沿射线A1O下滑,直至顶点B1落在x轴上时停止.设正方形落在x轴上方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围.
个单位长度的速度沿射线A1O下滑,直至顶点B1落在x轴上时停止.设正方形落在x轴上方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围.
解:(1)①∵四边形A1B1C1O为正方形,
∴OC1=B1C1,∠OC1B1=90度.
又∵D是B1C1的中点,
∴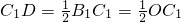 .
.
∵由旋转性质可知,∠C1OD=∠AOA1=α,
∴在Rt△C1OD中,tanα=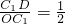 .
.
∴tanα的值是 .
.
 ②过点A1作A1E⊥x轴,垂足为点E.
②过点A1作A1E⊥x轴,垂足为点E.
在Rt△A1EO中,tanα=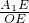 ,
,
∴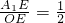 .
.
设A1E=k,则OE=2k,在Rt△A1EO中, ,
,
根据勾股定理,得A1E2+OE2=OA12.
即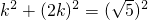 ,
,
解得k1=-1(舍),k2=1.
∴A1E=1,OE=2.
又∵点A1在第二象限,
∴点A1的坐标为(-2,1).
直接写出点B1的坐标为(-1,3),点C1的坐标为(1,2).
∵抛物线y=ax2+bx+c过点A1,B1,C1.
∴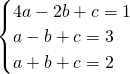
解得
∴抛物线的函数表达式为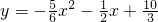 .
.
 (2)将(1)的抛物线解析式配方,得
(2)将(1)的抛物线解析式配方,得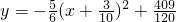 .
.
∴抛物线的对称轴是直线 .
.
假设存在符合条件的点P,分三种情况:
①以点B1为直角顶点;
易求得,直线A1B1的解析式:y=2x+5,
当x=- 时,y=2×(-
时,y=2×(- )+5=
)+5= ;
;
②以点C1为直角顶点;
易求得,直线OC1的解析式:y=2x,
当x=- 时,y=2×(-
时,y=2×(- )=-
)=- ;
;
③以点P为直角顶点;
分别过点B1、C1作抛物线对称轴的垂线,垂足为G、H;(如右图)
设点P(- ,y):
,y):
当点P在直线B1C1上方时,
B1G=1- =
= 、PG=y-3、C1H=1+
、PG=y-3、C1H=1+ =
= 、PH=y-2
、PH=y-2
∵∠B1PG=90°-∠C1PH=∠PC1H,∠B1GP=∠PHC1=90°
∴△B1GP∽△PHC1,则
解得:y=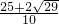 、y=
、y=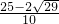 (舍);
(舍);
当点P在直线B1C1下方时,同上,可求得y=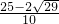 ;
;
综上,存在点P,使△PB1C1为直角三角形.
满足条件的点P共有4个: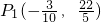 ,
,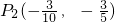 ,
, ,
,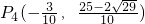 .
.
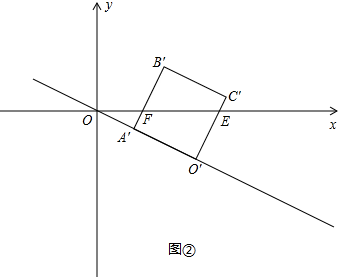
 (3)设运动后的正方形为O′A′B′C′,分三种情况:
(3)设运动后的正方形为O′A′B′C′,分三种情况:
①当点A′运动到x轴上时,t= ;
;
当0<t≤ 时,如图①;
时,如图①;
OO′=2 t,O′E=
t,O′E= OO′=
OO′= t
t
∴S=S正方形-S△OO′E=5- ×2
×2 t×
t× t=-5t2+5;
t=-5t2+5;
②当点C′运动到x轴上时,t=1;
当 <t<1时,如图②;
<t<1时,如图②;
OO′=2 t,OA′=2
t,OA′=2 t-
t- ,A′F=
,A′F= OA′=
OA′=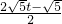 ,O′E=
,O′E= OO′=
OO′= t
t
B′F=A′B′-A′F=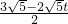 ,C′E=O′C′-O′E=
,C′E=O′C′-O′E= -
- t;
t;
∴S= (B′F+C′E)×B′C′=
(B′F+C′E)×B′C′= (
(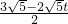 +
+ -
- t)×
t)× =
=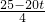 ;
;
③当点B′运动到x轴上时,t= ;
;
当1≤t< 时,如图③;
时,如图③;
同②可得:B′F=A′B′-A′F=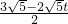 ,B′E=2B′F=3
,B′E=2B′F=3 -2
-2 t;
t;
∴S= ×
×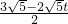 ×(3
×(3 -2
-2 t)=5t2-15t+
t)=5t2-15t+ ;
;
综上,S=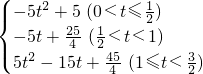 .
.
分析:(1)①在Rt△ODC1中,由旋转的性质知,∠DOC1=α,而DC1是正方形边长的一半,可据此求出∠α的正切值;
②在求抛物线的解析式中,必须先求出A1、B1、C1三点的坐标,可过这三点分别作坐标轴的垂线(具体向哪条坐标轴作垂线,可视情况而定),通过构建的直角三角形以及∠α的正切值,可求出这三点的坐标,再利用待定系数法求函数解析式即可.
(2)首先要大致确定有几个符合条件的点P:
①点B1是直角顶点,那么点P必为直线A1B1与抛物线对称轴的交点(有一个);
②点C1是直角顶点,那么点P必为直线OC1与抛物线对称轴的交点(有一个);
③点P是直角顶点,那么点P必为以线段B1C1为直径的圆与抛物线对称轴的交点(有两个),可过B1、C1作对称轴的垂线,通过构建的相似三角形来求出点P的坐标.
(3)此题的思路并不复杂,但需要考虑的情况较多,大致分成三段考虑即可:
①x轴在O、A1两点之间、②x轴在A1、C1两点之间、③x轴在B1、C1两点之间.
点评:此题涉及的内容相等复杂,难度很大,主要考查的知识点有:函数解析式的确定、正方形的性质、图形的旋转、解直角三角形的应用、相似三角形与直角三角形的判定和性质以及图形面积的解法等等.后两题涉及的情况较多,一定要注意分类讨论.最后一题中,一定要注意t的不同取值范围内,正方形的运动位置.
∴OC1=B1C1,∠OC1B1=90度.
又∵D是B1C1的中点,
∴
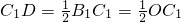 .
.∵由旋转性质可知,∠C1OD=∠AOA1=α,
∴在Rt△C1OD中,tanα=
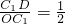 .
.∴tanα的值是
 .
. ②过点A1作A1E⊥x轴,垂足为点E.
②过点A1作A1E⊥x轴,垂足为点E.在Rt△A1EO中,tanα=
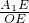 ,
,∴
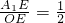 .
.设A1E=k,则OE=2k,在Rt△A1EO中,
 ,
,根据勾股定理,得A1E2+OE2=OA12.
即
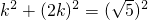 ,
,解得k1=-1(舍),k2=1.
∴A1E=1,OE=2.
又∵点A1在第二象限,
∴点A1的坐标为(-2,1).
直接写出点B1的坐标为(-1,3),点C1的坐标为(1,2).
∵抛物线y=ax2+bx+c过点A1,B1,C1.
∴
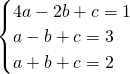
解得

∴抛物线的函数表达式为
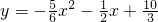 .
. (2)将(1)的抛物线解析式配方,得
(2)将(1)的抛物线解析式配方,得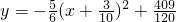 .
.∴抛物线的对称轴是直线
 .
.假设存在符合条件的点P,分三种情况:
①以点B1为直角顶点;
易求得,直线A1B1的解析式:y=2x+5,
当x=-
 时,y=2×(-
时,y=2×(- )+5=
)+5= ;
;②以点C1为直角顶点;
易求得,直线OC1的解析式:y=2x,
当x=-
 时,y=2×(-
时,y=2×(- )=-
)=- ;
;③以点P为直角顶点;
分别过点B1、C1作抛物线对称轴的垂线,垂足为G、H;(如右图)
设点P(-
 ,y):
,y):当点P在直线B1C1上方时,
B1G=1-
 =
= 、PG=y-3、C1H=1+
、PG=y-3、C1H=1+ =
= 、PH=y-2
、PH=y-2∵∠B1PG=90°-∠C1PH=∠PC1H,∠B1GP=∠PHC1=90°
∴△B1GP∽△PHC1,则

解得:y=
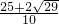 、y=
、y=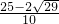 (舍);
(舍);当点P在直线B1C1下方时,同上,可求得y=
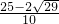 ;
;综上,存在点P,使△PB1C1为直角三角形.
满足条件的点P共有4个:
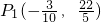 ,
,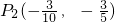 ,
, ,
,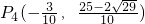 .
. (3)设运动后的正方形为O′A′B′C′,分三种情况:
(3)设运动后的正方形为O′A′B′C′,分三种情况:①当点A′运动到x轴上时,t=
 ;
;当0<t≤
 时,如图①;
时,如图①;OO′=2
 t,O′E=
t,O′E= OO′=
OO′= t
t∴S=S正方形-S△OO′E=5-
 ×2
×2 t×
t× t=-5t2+5;
t=-5t2+5;②当点C′运动到x轴上时,t=1;
当
 <t<1时,如图②;
<t<1时,如图②;OO′=2
 t,OA′=2
t,OA′=2 t-
t- ,A′F=
,A′F= OA′=
OA′=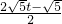 ,O′E=
,O′E= OO′=
OO′= t
tB′F=A′B′-A′F=
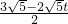 ,C′E=O′C′-O′E=
,C′E=O′C′-O′E= -
- t;
t;∴S=
 (B′F+C′E)×B′C′=
(B′F+C′E)×B′C′= (
(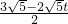 +
+ -
- t)×
t)× =
=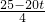 ;
;③当点B′运动到x轴上时,t=
 ;
;当1≤t<
 时,如图③;
时,如图③;同②可得:B′F=A′B′-A′F=
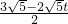 ,B′E=2B′F=3
,B′E=2B′F=3 -2
-2 t;
t;∴S=
 ×
×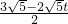 ×(3
×(3 -2
-2 t)=5t2-15t+
t)=5t2-15t+ ;
;综上,S=
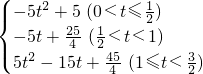 .
.

分析:(1)①在Rt△ODC1中,由旋转的性质知,∠DOC1=α,而DC1是正方形边长的一半,可据此求出∠α的正切值;
②在求抛物线的解析式中,必须先求出A1、B1、C1三点的坐标,可过这三点分别作坐标轴的垂线(具体向哪条坐标轴作垂线,可视情况而定),通过构建的直角三角形以及∠α的正切值,可求出这三点的坐标,再利用待定系数法求函数解析式即可.
(2)首先要大致确定有几个符合条件的点P:
①点B1是直角顶点,那么点P必为直线A1B1与抛物线对称轴的交点(有一个);
②点C1是直角顶点,那么点P必为直线OC1与抛物线对称轴的交点(有一个);
③点P是直角顶点,那么点P必为以线段B1C1为直径的圆与抛物线对称轴的交点(有两个),可过B1、C1作对称轴的垂线,通过构建的相似三角形来求出点P的坐标.
(3)此题的思路并不复杂,但需要考虑的情况较多,大致分成三段考虑即可:
①x轴在O、A1两点之间、②x轴在A1、C1两点之间、③x轴在B1、C1两点之间.
点评:此题涉及的内容相等复杂,难度很大,主要考查的知识点有:函数解析式的确定、正方形的性质、图形的旋转、解直角三角形的应用、相似三角形与直角三角形的判定和性质以及图形面积的解法等等.后两题涉及的情况较多,一定要注意分类讨论.最后一题中,一定要注意t的不同取值范围内,正方形的运动位置.

练习册系列答案
相关题目
 如图,正方形ABCO放在平面直角坐标系中,其中点O为坐标原点,A、C两点分别在x轴的负半轴和y轴的正半轴上,点B的坐标为(-4,4).已知点E、点F分别从A、点B同时出发,点E以每秒2个单位长度的速度在线段AB上来回运动.点F沿B→C→0方向,以每秒1个单位长度的速度向点O运动,当点F到达点O时,E、F两点都停止运动.在E、F的运动过程中,存在某个时刻,使得△OEF的面积为6.那么点E的坐标为
如图,正方形ABCO放在平面直角坐标系中,其中点O为坐标原点,A、C两点分别在x轴的负半轴和y轴的正半轴上,点B的坐标为(-4,4).已知点E、点F分别从A、点B同时出发,点E以每秒2个单位长度的速度在线段AB上来回运动.点F沿B→C→0方向,以每秒1个单位长度的速度向点O运动,当点F到达点O时,E、F两点都停止运动.在E、F的运动过程中,存在某个时刻,使得△OEF的面积为6.那么点E的坐标为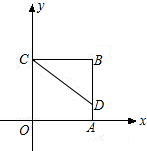 如图,正方形ABCO的边长为4,D为AB上一点,且BD=3,以点C为中心,把△CBD顺时针旋转90°,得到△CB1D1.
如图,正方形ABCO的边长为4,D为AB上一点,且BD=3,以点C为中心,把△CBD顺时针旋转90°,得到△CB1D1. 如图,正方形ABCO的边长是2,E是BC中点,则E点的坐标是
如图,正方形ABCO的边长是2,E是BC中点,则E点的坐标是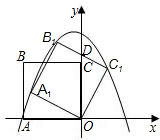 B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.
B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1、B1、C1.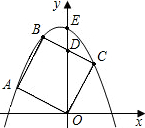 x2+bx+c经过B、C且与y轴的交点为
x2+bx+c经过B、C且与y轴的交点为