题目内容
 如图,在△ABC的三边AB,BC,CA的长分别为30,20,20,O为三边角平分线的交点,则△ABO,△BCO,△ACO的面积比等于( )
如图,在△ABC的三边AB,BC,CA的长分别为30,20,20,O为三边角平分线的交点,则△ABO,△BCO,△ACO的面积比等于( )分析:根据角平分线上的点到角的两边的距离相等可得点O到AB、BC、AC的距离相等,再根据等高三角形的面积的比等于底边的比可得三个三角形的面积的比等于AB、BC、AC的比,然后进行计算即可得解.
解答:解:∵O为三边角平分线的交点,
∴点O到AB、BC、AC的距离相等,
∵AB,BC,CA的长分别为30,20,20,
∴△ABO,△BCO,△ACO的面积比=30:20:20=3:2:2.
故选D.
∴点O到AB、BC、AC的距离相等,
∵AB,BC,CA的长分别为30,20,20,
∴△ABO,△BCO,△ACO的面积比=30:20:20=3:2:2.
故选D.
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,等高的三角形的面积的比等于相应底边的比.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 如图,将△ABC的三个顶点与同一个内点连接起来,所得三条连线把△ABC分成六个小三角形,其中四个小三角形面积在图中已标明,则△ABC的面积为
如图,将△ABC的三个顶点与同一个内点连接起来,所得三条连线把△ABC分成六个小三角形,其中四个小三角形面积在图中已标明,则△ABC的面积为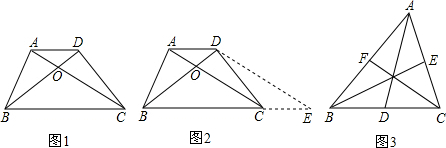
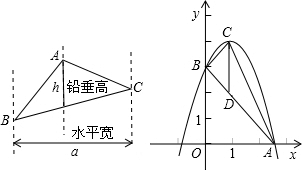

 阅读材料:
阅读材料: