题目内容
已知直线y=(n+1)x-n2+2n+5过点(0,-3),且它对应的函数值y随x的增大而减小,求n的值.
解:∵直线y=(n+1)x-n2+2n+5过点(0,-3),
∴-n2+2n+5=-3,
整理得,n2-2n-8=0,
解得n1=-2,n2=4,
∵函数值y随x的增大而减小,
∴n+1<0,
解得n<-1,
所以,n的值为-2.
分析:把点(0,-3)代入直线解析式,解关于n的一元二次方程求出n的值,再根据函数值y随x的增大而减小列出不等式n+1<0,求解即可作出判断.
点评:本题考查了一次函数图象上点的坐标特征,以及一次函数的增减性,一元二次方程的解法,要注意根据增减性求出n的取值范围,这也是本题容易忽视而导致出错的地方.
∴-n2+2n+5=-3,
整理得,n2-2n-8=0,
解得n1=-2,n2=4,
∵函数值y随x的增大而减小,
∴n+1<0,
解得n<-1,
所以,n的值为-2.
分析:把点(0,-3)代入直线解析式,解关于n的一元二次方程求出n的值,再根据函数值y随x的增大而减小列出不等式n+1<0,求解即可作出判断.
点评:本题考查了一次函数图象上点的坐标特征,以及一次函数的增减性,一元二次方程的解法,要注意根据增减性求出n的取值范围,这也是本题容易忽视而导致出错的地方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
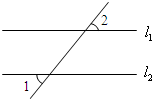 (2007•黔南州)如图,已知直线l1∥l2,∠1=50°,那么∠2=
(2007•黔南州)如图,已知直线l1∥l2,∠1=50°,那么∠2= (2012•株洲模拟)如图,已知直线AB是⊙O的切线,A为切点,OB交⊙O于点C,点D在⊙O上,且∠OBA=40°,则∠ADC的度数为( )
(2012•株洲模拟)如图,已知直线AB是⊙O的切线,A为切点,OB交⊙O于点C,点D在⊙O上,且∠OBA=40°,则∠ADC的度数为( )
 如图,已知直线AB∥CD,直线EF截AB、CD于E、F,EG⊥CD,∠EFD=45°且FG=8,则AB、CD之间的距离为
如图,已知直线AB∥CD,直线EF截AB、CD于E、F,EG⊥CD,∠EFD=45°且FG=8,则AB、CD之间的距离为