Question

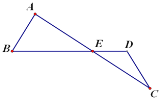
【题目】如图，在△ABE中，∠B=60°，AB=8，C、D分别是△ABE的边AE延长线上和边BE延长线上两点，连接CD，∠A-∠C=60°，AB=CD，DE=6，则线段AC的长度等于______.

Answer 1

【答案】

【解析】

过点A 作AF∥CD交BE于点F，AG⊥BD，交BD于点G，由AF∥CD得出

∠FAE=∠ECD，进而得出△ABF为等边三角形，再通过证明△AEF≌△CED，得出EF=DE=6，求出AG的长，在Rt△AGE中，利用勾股定理即可求解.

如图，过点A 作AF∥CD交BE于点F，AG⊥BD，交BD于点G，

∵AF∥CD，

∴∠FAE=∠ECD，

∵，

∴∠BAF=60°，

∵∠B=60°，

∴△ABF为等边三角形，

∴AB=AF，

∵AB=CD，

∴AF=CD，

又∵∠FAE=∠ECD，∠AEF=∠CED，

∴△AEF≌△CED，

∴EF=DE=6，

∵AB=8，BG=4，

∴，

∴，

∴.

故答案为.