题目内容
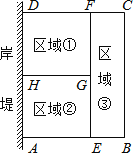
【题目】为了节省材料,小浪底水库养殖户小李利用水库的岸堤(足够长)为一边,用总长为120米的网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)请你帮养殖户小李计算一下BC边多长时,养殖区ABCD面积最大,最大面积为多少?
【答案】(1)y=-![]() x2+45x,(0<x<60);(2)当BC为30米时,养殖区ABCD面积最大,最大面积为675平方米.
x2+45x,(0<x<60);(2)当BC为30米时,养殖区ABCD面积最大,最大面积为675平方米.
【解析】
(1)根据矩形面积相等得到边长的关系,然后用含x的式子表示相关边长,根据矩形的面积公式即可得到答案;
(2)将方程化成顶点式:y=-![]() x2+45x=-
x2+45x=-![]() (x-30)2+675即可求解.
(x-30)2+675即可求解.
(1)∵三个矩形的面积相等,
∴2FG=2GE=BC,
∴![]() BC×DF=BC×FC,
BC×DF=BC×FC,
∴2FC=DF,
∴2BC+8FC=120,
∴FC=![]() ,
,
∴y与x之间的函数关系式为y=3FC×BC=3×![]() ·x,
·x,
即y=-![]() x2+45x,(0<x<60);
x2+45x,(0<x<60);
(2)y=-![]() x2+45x=-
x2+45x=-![]() (x-30)2+675,
(x-30)2+675,
则当BC为30米时,养殖区ABCD面积最大,最大面积为675平方米.

练习册系列答案
相关题目
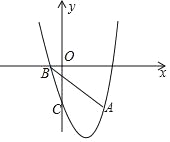
【题目】对于抛物线![]() .
.
(1)它与x轴交点的坐标为 ,与y轴交点的坐标为 ,顶点坐标为 ;
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |

(3)利用以上信息解答下列问题:若关于x的一元二次方程![]() (t为实数)在
(t为实数)在![]() <x<
<x<![]() 的范围内有解,则t的取值范围是 .
的范围内有解,则t的取值范围是 .