题目内容
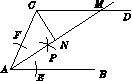
如图14,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于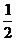 EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN.
(1)解:∵AB∥CD,∴∠ACD+∠CAB=180°.
又∵∠ACD=114°,∴∠CAB=66°.由作法知,AM是∠CAB的平分线,∴∠MAB=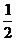 ∠CAB=33°.
∠CAB=33°.
(2)证明:∵AM平分∠CAB,∴∠CAM=∠MAB. ∵AB∥CD,
∴∠MAB=∠CMA.∴∠CAN=∠CMN.又∵CN⊥AM,∴∠ANC=
∠MNC.在△ACN和△MCN中,∵∠ANC=∠MNC,∠CAN=∠CMN,CN=CN,∴△ACN≌△MCN(AAS).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .试说明不论
.试说明不论 为何使分式有意义
为何使分式有意义 = .
= . 和△
和△ 中,
中, =
= ,且
,且 ,
, ,则这两个三角形( )
,则这两个三角形( )

 与多项式
与多项式 的公因式是________.
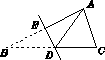
的公因式是________. 纸片沿
纸片沿 折叠,当点
折叠,当点 落在四边形
落在四边形 内部时,则
内部时,则 与
与 之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
 B.
B.
 D.
D.