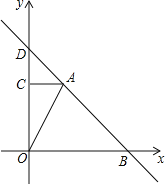��Ŀ����
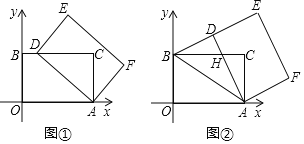
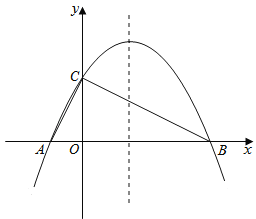
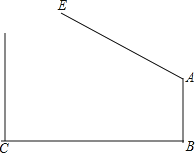
����Ŀ��ij��˾���ų��ڴ���һ�Զ���Ӧ���ˣ���A������ת����֧�㣬����������ʱ������AE���Զ�����ij�����ϣ����˷������ϣ���ij��λ��ͻȻ��ס����ʱ�����������ĽǶȡ�BAE��127������֪AB��BC��֧��AB��1.2�ף�����BC�Ŀ���Ϊ2�ף���ʱһ�������߷ֱ�Ϊ(4600 mm��1700 mm��1400 mm)�������ܷ�˳��ͨ����(���˿��ȣ��������⾵���Բ��ƣ��ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��)
���𰸡���ͨ��.
��������
����������ֻҪ����������ʻ���������߶�С��AȨ��ĸ߶�NQ������ͨ�������������жϵó����ɣ�
��ͼ������A��BC��ƽ����AG������N��NQ��BC��Q����AG�ڵ�R��
���BAG=90�㣬

�ߡ�BAE=127�㣬��BAG=90�㣬
���EAH=��EAB-��BAG=37�㣮
����NAR�У���ARN=90�㣬��EAG=37�㣬
������Ϊ1.7m����GR=1.7m����AR=2-1.7=0.3��m����
��NR=ARtan37��=0.3��0.75=0.225��m����
��NQ=1.2+0.225=1.425��1.4��
����ߣ�4600mm��1700mm��1400mm������ͨ��.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
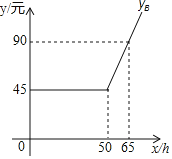
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ijͨ�Ź�˾����![]() �������������շѷ�ʽ��
�������������շѷ�ʽ��
�շѷ�ʽ | ��ʹ�÷�/Ԫ | ��ʱ����ʱ��/ | ��ʱ��/��Ԫ/ |
| 30 | 25 | 0.05 |
|
|
|
|
��ÿ������ʱ��Ϊ![]() ����ʽ
����ʽ![]() ���շѽ��ֱ�Ϊ
���շѽ��ֱ�Ϊ![]() ��Ԫ����
��Ԫ����![]() ��Ԫ������ͼ��
��Ԫ������ͼ��![]() ��
��![]() ֮�亯����ϵ��ͼ��������ʾ�����ۼ�����ʱ�䲻������ʱ����ʱ�䣬��ֻ����ʹ�÷ѣ����ۼ�����ʱ�䳬����ʱ����ʱ�䣬��Գ��������ټ��ճ�ʱ�ѣ�
֮�亯����ϵ��ͼ��������ʾ�����ۼ�����ʱ�䲻������ʱ����ʱ�䣬��ֻ����ʹ�÷ѣ����ۼ�����ʱ�䳬����ʱ����ʱ�䣬��Գ��������ټ��ճ�ʱ�ѣ�
��1��![]() ��
��![]() ��
��![]() ��
��
��2����![]() ֮��ĺ�������ʽ��
֮��ĺ�������ʽ��
��3����ÿ������ʱ��Ϊ31Сʱ����ֱ��д��ѡ�����ַ�ʽ�ܽ�ʡ�����ѣ�