题目内容
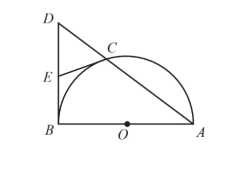
【题目】如图，AB 为半⊙O 的直径，弦 AC 的延长线与过点 B 的切线交于点 D，E 为 BD的中点，连接 CE．
（1）求证：CE 为 O 的切线；
（2）过点 C 作 CF AB ，垂足为点 F，AC=5，CF=3，求⊙O的半径．
【答案】（1）证明见解析（2）
【解析】
(1) 连接CO、EO、BC,可证的△EBOP≌△ECO，可得∠ECO=∠EBO=90°，所以CE为⊙O的切线；
（2）设：BF=x，利用勾股定理BC2+AC2=AB2可求出x的值，可得圆的半径.
(1)连接CO、EO、BC
∵AB是直径
∴∠BCA=∠BCD=90°
∵RtABCD中E为BD中点
∴CE=BE=ED
则△EBOP≌△ECO(SSS)
∠ECO=∠EBO=90°
∵点C在圆上
∴CE为⊙O的切线
（2）由题意得：AF=4
设：BF=x
利用勾股定理BC2=x2+32
BC2+AC2=AB2
x2+32+52=(x+4)2
解得：
则
则⊙O的半径为
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】某校数学兴趣小组，对函数y＝|x﹣1|+1的图象和性质进行了探究，探究过程如下：
（1）自变量x的取值范围是全体实数，x与y的几组对应值如表：
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 5 | 4 | m | 2 | 1 | 2 | 3 | 4 | 5 | … |
其中m＝ ．
（2）如图，在平面直角坐标系xOy中，描出了上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象：
（3）根据画出的函数图象特征，仿照示例，完成下列表格中的函数变化规律：
序号 | 函数图象特征 | 函数变化规律 |
示例1 | 在直线x＝1的右侧，函数图象呈上升状态 | 当x＞1时，y随x的增大而增大 |
① | 在直线x＝1的左侧，函数图象呈下降状态 |
|
示例2 | 函数图象经过点（﹣3，5） | 当x＝﹣3时，y＝5 |
② | 函数图象的最低点是（1，1） |
|
（4）当2＜y≤4时，x的取值范围为 ．
